Chương 1. Ứng dụng đạo hàm
Bài 3. Đường tiệm cận của đồ thị hàm số
Lý thuyết
Đường tiệm cận ngang
- Đường thẳng $y=y_0$ gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số $y=f(x)$ nếu \(\lim_{x\to +\infty}f(x)=y_0 \text{ hoặc } \lim_{x\to - \infty}f(x)=y_0.\)
Đường tiệm cận đứng
- Đường thẳng $x=x_0$ gọi là đường tiệm cận đướng (gọi tắt là tiệm cận đứng) của đồ thị hàm số $y=f(x)$ nếu ít nhất một trong các điều kiện sau được thỏa mãn:
\(\left[ \begin{array}{l}
\lim\limits_{x\to x_o^+}f(x)=+\infty; \\\\
\lim\limits_{x\to x_o^+}f(x)=-\infty; \\\\
\lim\limits_{x\to x_o^-}f(x)=+\infty; \\\\
\lim\limits_{x\to x_o^-}f(x)=-\infty; \\\\
\end{array} \right.\)
Đường tiệm cận xiên
- Đường thẳng $y=ax+b(a\neq 0)$ gọi là đường tiệm cận xiên (gọi tắt là tiệm cận xiên) của đồ thị hàm số $y=f(x)$ nếu \(\lim_{x\to +\infty}[f(x)-(ax+b)]=0 \text{ hoặc } \lim_{x\to -\infty}[f(x)-(ax+b)]=0.\)
Các dạng bài tập
Dạng 1. Tìm các đường tiệm cận khi cho bảng biến thiên - đồ thị
Phương pháp
-
Bước 1: Tìm tập xác định của hàm số. Giả sử
\(D = (-\infty; +\infty) \setminus \\\{x_0\\\}.\) -
Bước 2: Quan sát Bảng biến thiên hoặc đồ thị, tìm giới hạn
-
Nếu
\(\lim_{x \to +\infty} y = y_0 \quad \text{hoặc} \quad \lim_{x \to -\infty} y = y_0\)
thì $y = y_0$ là đường tiệm cận ngang của đồ thị hàm số. -
Nếu
\(\lim_{x \to x_0^+} y = \pm \infty \quad \text{hoặc} \quad \lim_{x \to x_0^-} y = \pm \infty\)
thì $x = x_0$ là đường tiệm cận đứng của đồ thị hàm số. - Nếu
\(\lim_{x \to +\infty} \Big[y - (ax+b)\Big] = 0 \quad \text{hoặc} \quad \lim_{x \to -\infty} \Big[y - (ax+b)\Big] = 0\) thì $y = ax+b$ là tiệm cận xiên của đồ thị hàm số.
Chú ý
- Nếu $\lim_{x \to +\infty} y = y_1$ và $\lim_{x \to -\infty} y = y_2$ thì ta có hai đường tiệm cận ngang: $y = y_1, y = y_2$.
- Nếu tập xác định không chứa $+\infty, -\infty$ thì đồ thị hàm số không có tiệm cận ngang.
- Nếu hàm số xác định trên $\mathbb{R}$ thì đồ thị không có tiệm cận đứng.
Ví dụ 1.1
Cho hàm số $y = f(x)$ có bảng biến thiên sau:
| $x$ | $-\infty$ | $0$ | $3$ | $+\infty$ | |||
|---|---|---|---|---|---|---|---|
| $y^\prime$ | $-$ | $||$ | $-$ | $0$ | $+$ | ||
| $y$ | $1$ | $\searrow$ | $||$ | $2$ $\searrow$ | $-3$ | $\nearrow$ | $3$ |
Ví dụ 1.2
Cho đồ thị hàm số $y=f(x)$ như hình bên dưới. Tìm tiệm cận đứng và tiệm cận xiên của đồ thị hàm số đã cho.
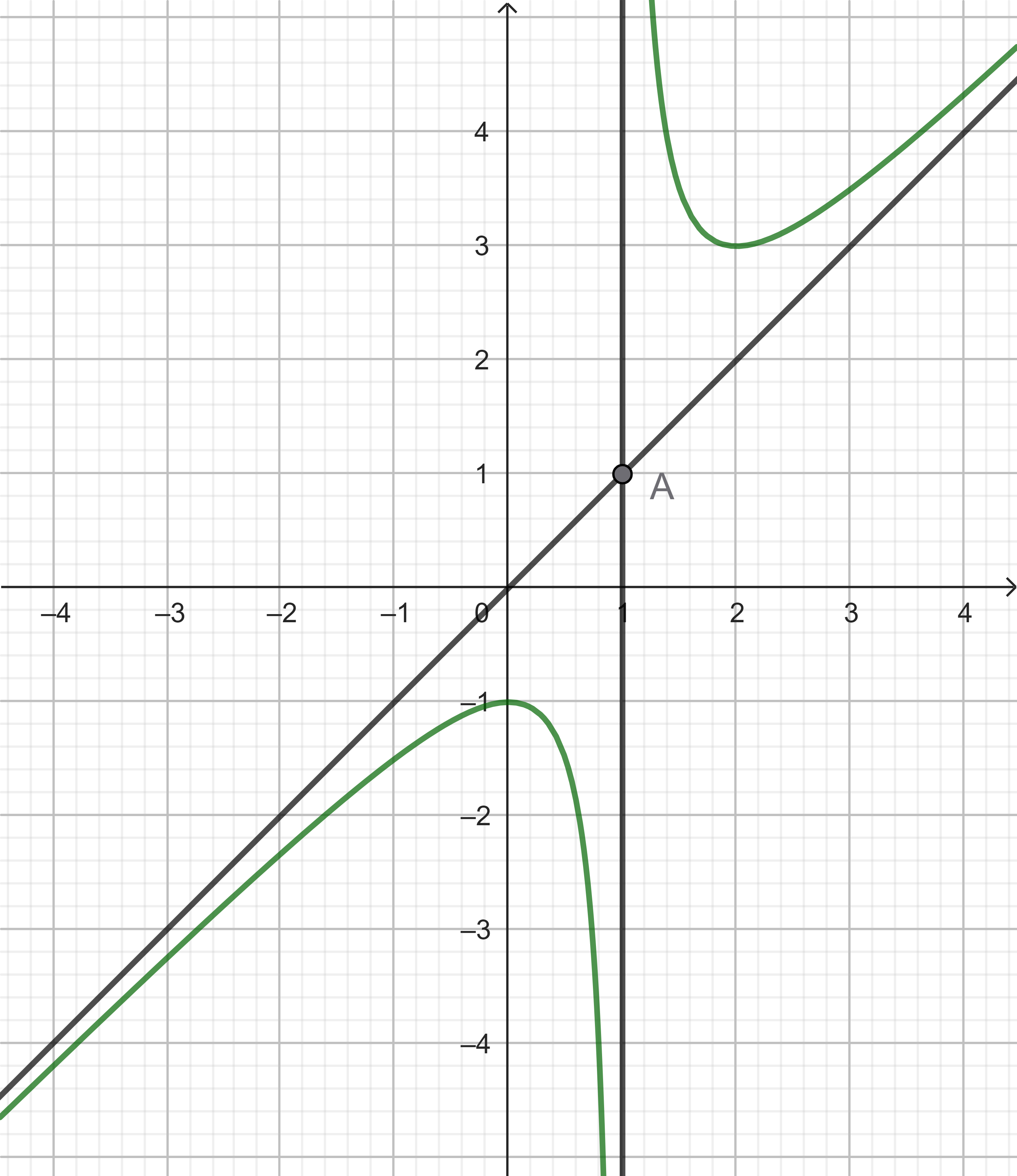
Ví dụ 1.3
Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên như sau
| $x$ | $-\infty$ | $-2$ | $-1$ | $-3$ | $+\infty$ | ||||
|---|---|---|---|---|---|---|---|---|---|
| $y^\prime$ | $-$ | $||$ | $+$ | $||$ | $+$ | $0$ | $-$ | ||
| $y$ | $5$ | $\searrow$ | $3$ | $\nearrow +\infty$ | $||$ | $-2\nearrow$ | $1$ | $\searrow$ | $-5$ |
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là bao nhiêu?
Dạng 2. Tìm các đường tiệm cận khi cho hàm số
Phương pháp
- Bước 1: Tìm tập xác định của hàm số.
- Bước 2: Tìm giới hạn tại các điểm vô cực và các điểm không xác định.
- Bước 3: Kết luận về các đường tiệm cận.
Ví dụ 2.1
Tìm các đường tiệm cận của đồ thị hàm số $y=\dfrac{2x-1}{x-1}$.
Ví dụ 2.2
Tìm các đường tiệm cận của đồ thị hàm số $y=\dfrac{x^2+1}{x}$.
Ví dụ 2.3
Tìm các đường tiệm cận của đồ thị hàm số $y=f(x)=\dfrac{x^3-x^2+1}{x^2-1}$.
Dạng 3. Đường tiệm cận liên quan góc – khoảng cách – diện tích
Phương pháp
- Bước 1: Xác định các đường tiệm cận của đồ thị hàm số.
- Bước 2: Dựa vào các giả thiết: khoảng cách, góc, diện tích,… để tính toán hoặc thiết lập phương trình, hệ phương trình để tìm ẩn cần tìm.
Ví dụ 3.1
Tìm các giá trị m để đồ thị hàm số $y = \dfrac{4mx + 3m}{x - 2}$ có đường tiệm cận đứng và tiệm cận ngang tạo với hai trục tọa độ một hình chữ nhật có diện tích bằng 2024?
Ví dụ 3.2
Cho hàm số $y = \dfrac{2x^2 - x}{x - 1}$ có đồ thị $(C)$.
(1) Tính khoảng cách từ $M(2;1)$ đến đường tiệm cận đứng của đồ thị hàm số $(C)$.
(2) Đường tiệm cận xiên của đồ thị hàm số $(C)$ cắt hai trục tọa độ lần lượt tại hai điểm $A$, $B$. Tính diện tích của tam giác $OAB$ đó.
Ví dụ 3.3
Cho hàm số $y = \dfrac{4x + 4}{3 - x}$ có đồ thị là $(C)$. Tìm giá trị nhỏ nhất của tổng các khoảng cách từ một điểm $M$ tùy ý trên $(C)$ đến hai đường tiệm cận của đồ thị hàm số $(C)$.
Dạng 4. Bài toán thực tế và ý nghĩa của giá trị gần về tiệm cận
Phương pháp
- Bước 1: Biểu diễn các đại lượng với nhau thông qua hàm số.
- Bước 2: Tìm tiệm cận của hàm số vừa tìm được.
- Bước 3: Nêu ý nghĩa của giá trị gần về tiệm cận.
Ví dụ 4.1
Để loại bỏ $x\%$ chất gây ô nhiễm không khí từ khí thải của một nhà máy, người ta ước tính chi phí cần bỏ ra là
\[C(x) = \dfrac{300x}{100-x} \text{ (triệu đồng)}, \quad 0 \le x < 100.\]Hãy cho biết: (1) Chi phí cần bỏ ra sẽ thay đổi như thế nào khi $x$ tăng?
(2) Có thể loại bỏ được 100% chất gây ô nhiễm không khí không? Vì sao?
Ví dụ 4.2
Số lượng sản phẩm bán được của một công ty sau $x$ tháng được tính theo công thức: \(S(x) = 200 \left(5 - \dfrac{9}{2 + x}\right), \quad x \ge 1.\)
(1) Xem $y = S(x)$ là một hàm số xác định trên nửa khoảng $[1; +\infty)$, hãy tìm tiệm cận ngang của đồ thị hàm số đó.
(2) Nêu nhận xét về số lượng sản phẩm bán được của công ty đó trong $x$ (tháng) khi $x$ đủ lớn.
Ví dụ 4.3
Một bể chứa 5000 lít nước tinh khiết. Nước muối có nồng độ 30 gam muối/lít được bơm vào bể với tốc độ 25 lít/phút.
(1) Chứng minh rằng nồng độ muối trong bể sau t phút (tính bằng tỷ lệ khối lượng muối trong bể với thể tích nước trong bể, đơn vị: g/L) được cho bởi hàm số $f(t) = \dfrac{30t}{200 + t}$.
(2) Xem $y = f(t)$ là một hàm số xác định trên đoạn $[0; +\infty)$, hãy tìm tiệm cận ngang của đồ thị hàm số đó.
(3) Nêu nhận xét về nồng độ muối trong bể khi thời gian $t$ tăng.