Chương 1. Ứng dụng đạo hàm

Bài 4. Khảo sát sự biến thiên và vẽ đồ thị của hàm số

A. Lý thuyết

1. Sơ đồ khảo sát hàm số

Các bước thực hiện:

1. Tìm tập xác định của hàm số

2. Khảo sát sự biến thiên của hàm số

   • Tính đạo hàm $y’$. Tìm các điểm tại đó $y’=0$ hoặc đạo hàm không tồn tại.

   • Xét dấu $y’$ để chỉ ra các khoảng đơn điệu của hàm số.

   • Tìm cực trị của hàm số.

   • Tìm các giới hạn tại vô cực, giới hạn vô cực và tìm tiệm cận của đồ thị hàm số (nếu có).

   • Lập bảng biến thiên của hàm số.

3. Vẽ đồ thị của hàm số dựa vào bảng biến thiên

   • Chú ý: Khi vẽ đồ thị, nên xác định thêm một số điểm đặc biệt của đồ thị:

   • Giao điểm của đồ thị với các trục tọa độ.

   • Trục đối xứng, tâm đối xứng (nếu có).

   • Giao điểm của đồ thị với các trục tọa độ.

   • Trục đối xứng, tâm đối xứng (nếu có).

   • Vẽ các đường tiệm cận của đồ thị hàm số (nếu có).

2. Khảo sát và vẽ đồ thị hàm số đa thức bậc 3: $y=ax^3=bx^2+cx+d (a\neq 0)$

• Tập xác định $D=R.$

• $y’=3ax^2+2bx+c$

• Xét dấu $y’$ có 3 trường hợp:

có 2 nghiệm	có nghiệm kép	vô nghiệm
2 cực trị	0 cực trị	không có cực trị

• Kết luận cực trị (nếu có)

• Tìm giới hạn tại vô cực

• Lập bảng biến thiên

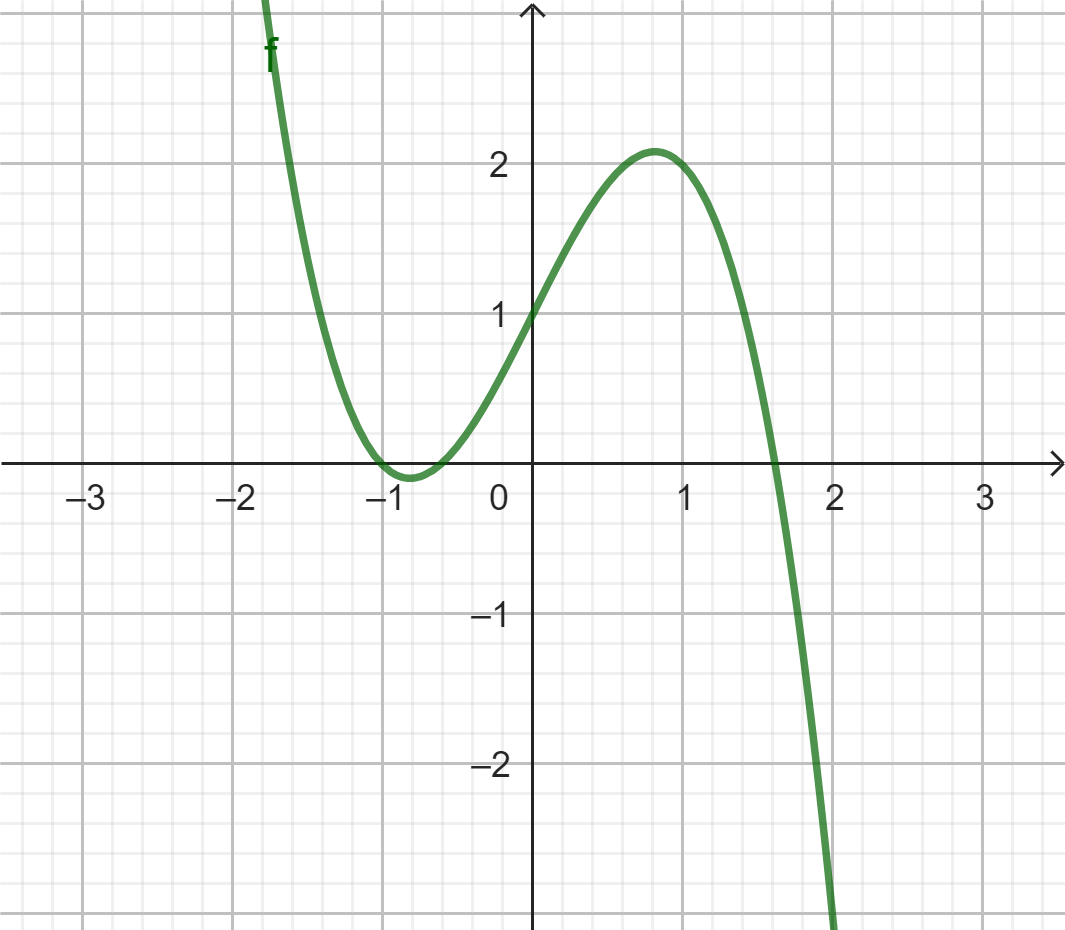
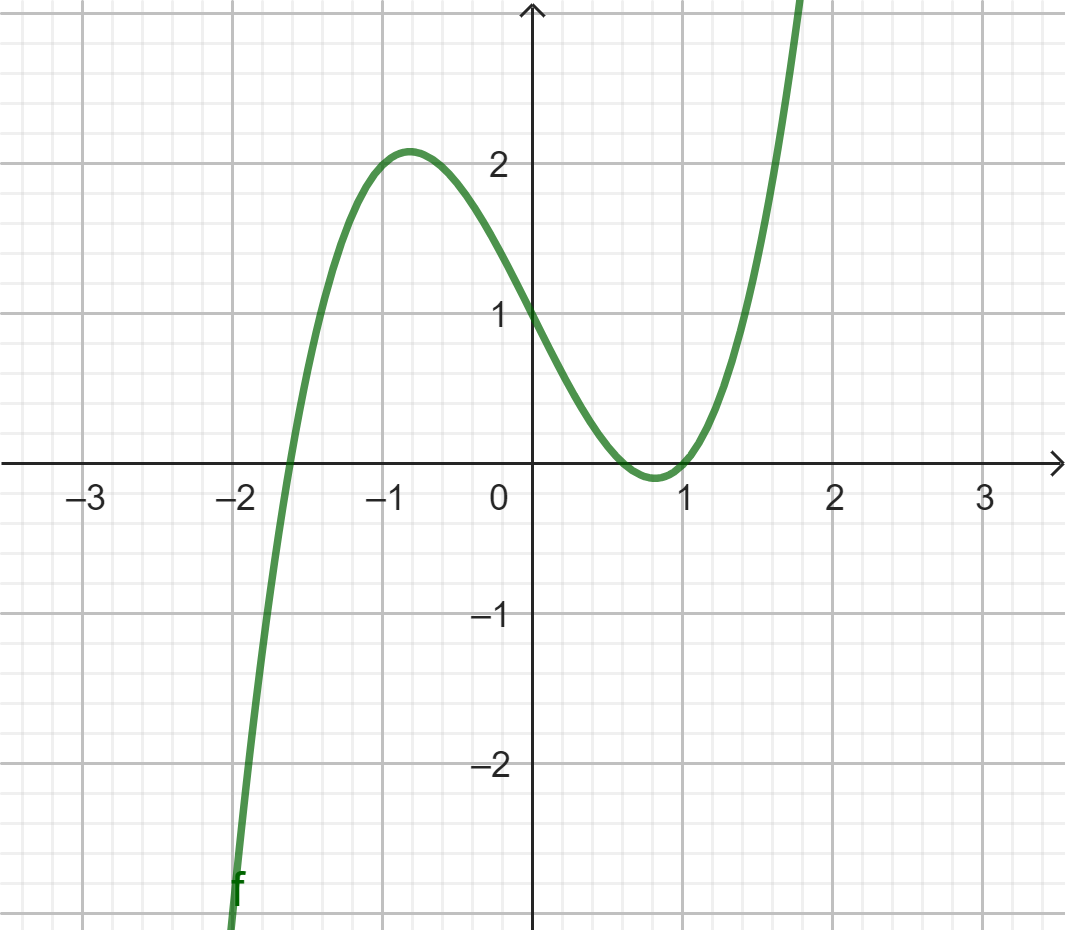
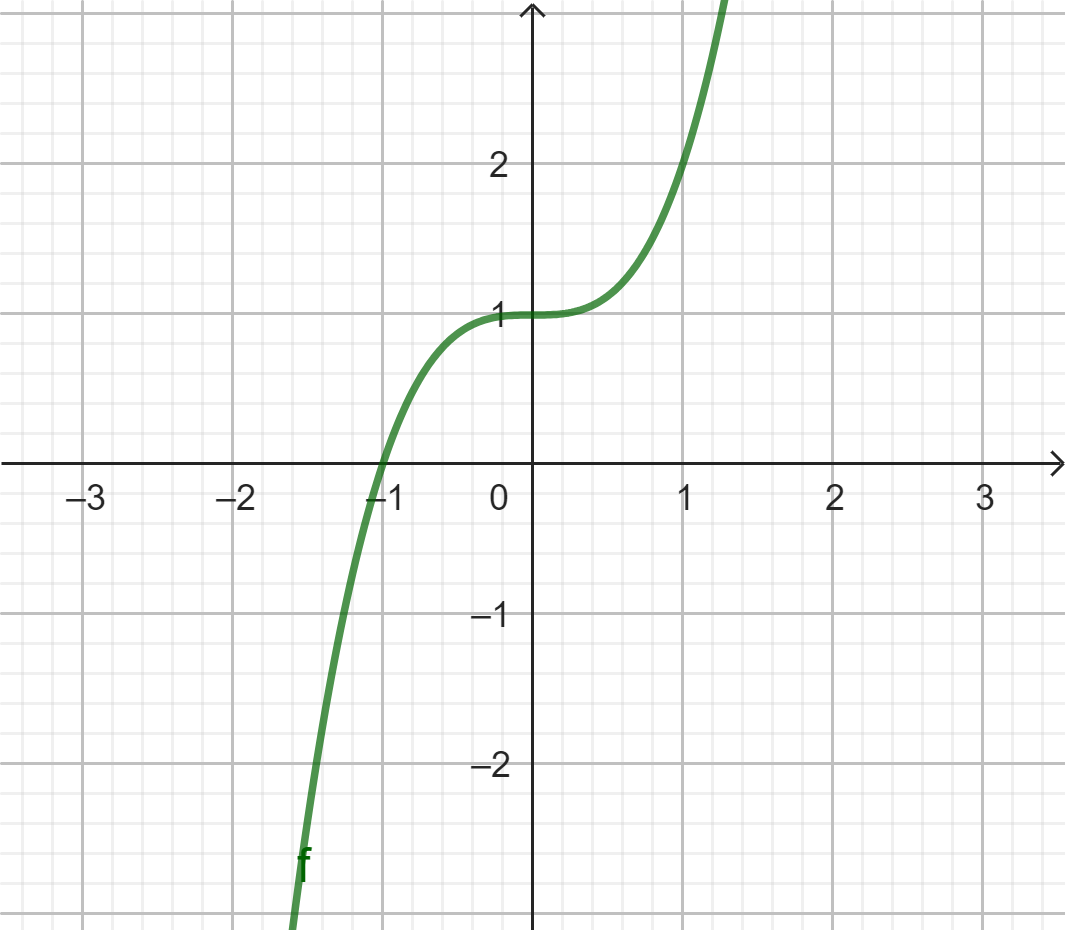
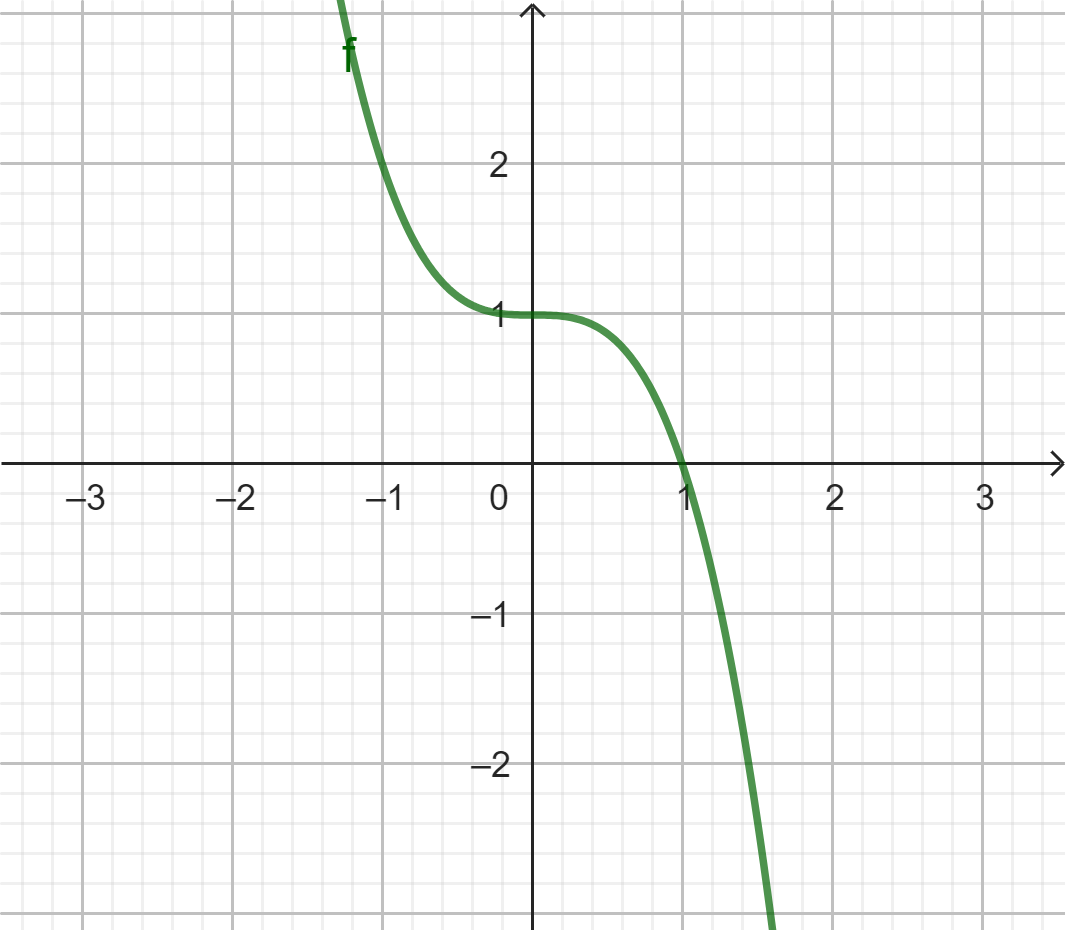
• Đồ thị: Có 4 dạng chính sau: ngã ngược, ngã xuôi, đi lên từ trái qua phải; đi xuống từ trái qua phải

• Đồ thị có tâm đối xứng là điểm uốn có hoành độ thỏa mãn $y’‘=0$ tức là $x=\frac{-b}{3a}.$

• Không có tiệm cận

3. Khảo sát và vẽ đồ thị hàm số phân thức hữu tỉ

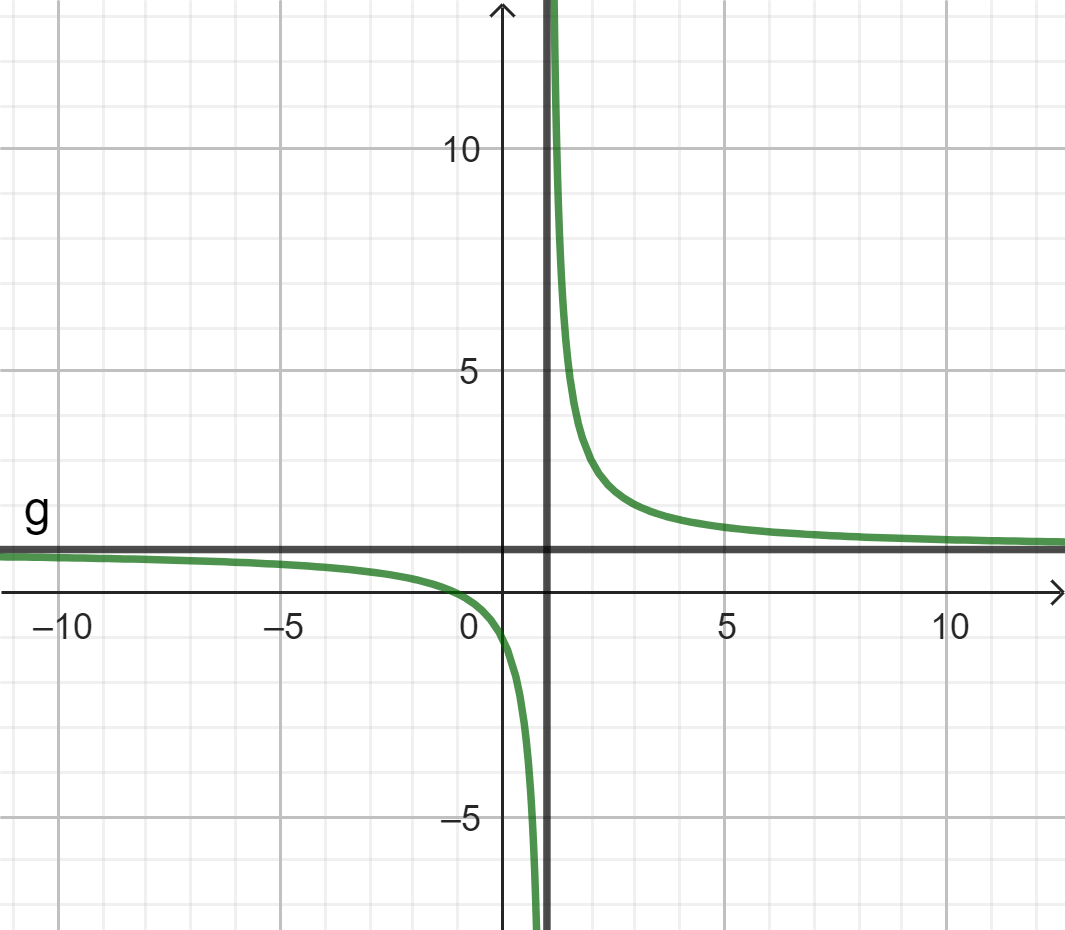
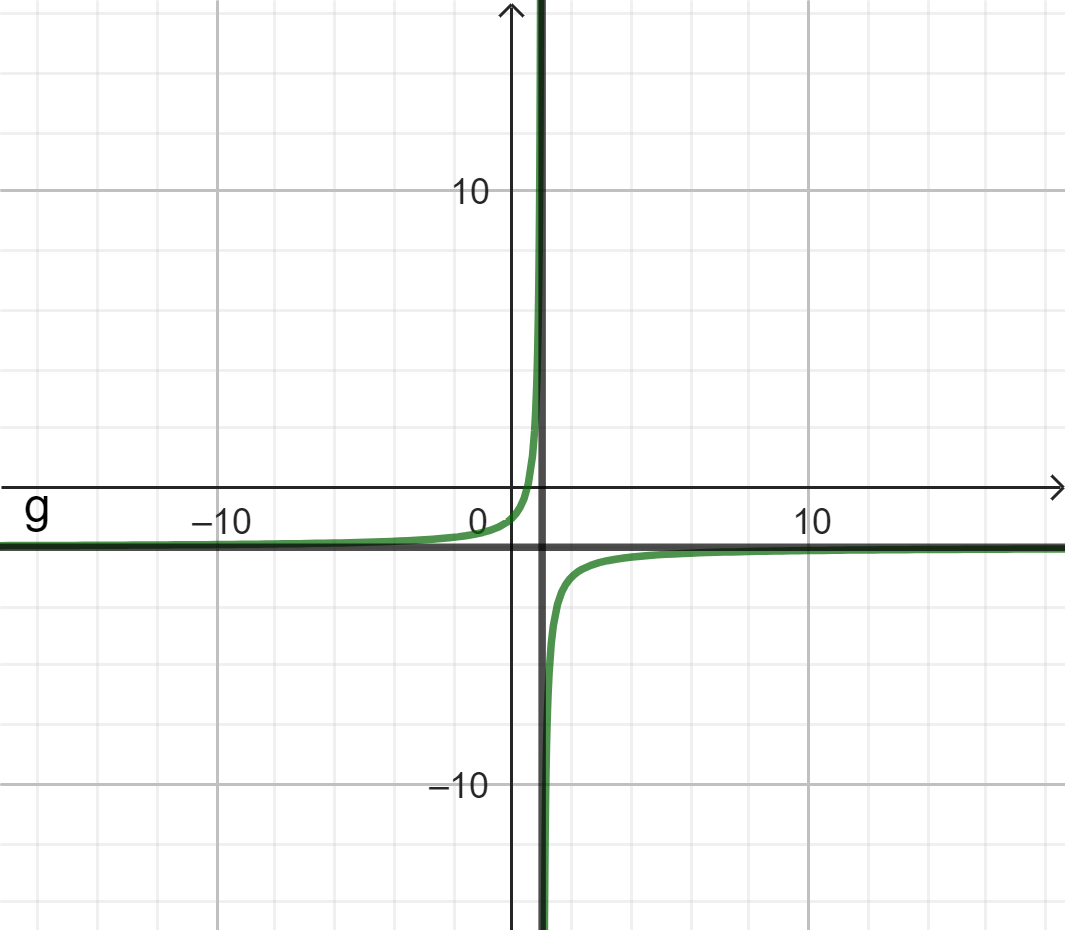
3.1. Dạng $y=\frac{ax+b}{cx+d}$.

• $D=R\setminus\{x=\frac{-d}{c}\}.$

• Có tiệm cận đứng $x=\frac{-d}{c}$ và tiệm cận ngang $y=\frac{a}{c}.$

• Chỉ đồng biến hoặc nghịch biến.

• Có tâm đối xứng $I(\frac{-d}{c};\frac{a}{c}).$

||| |—|—|

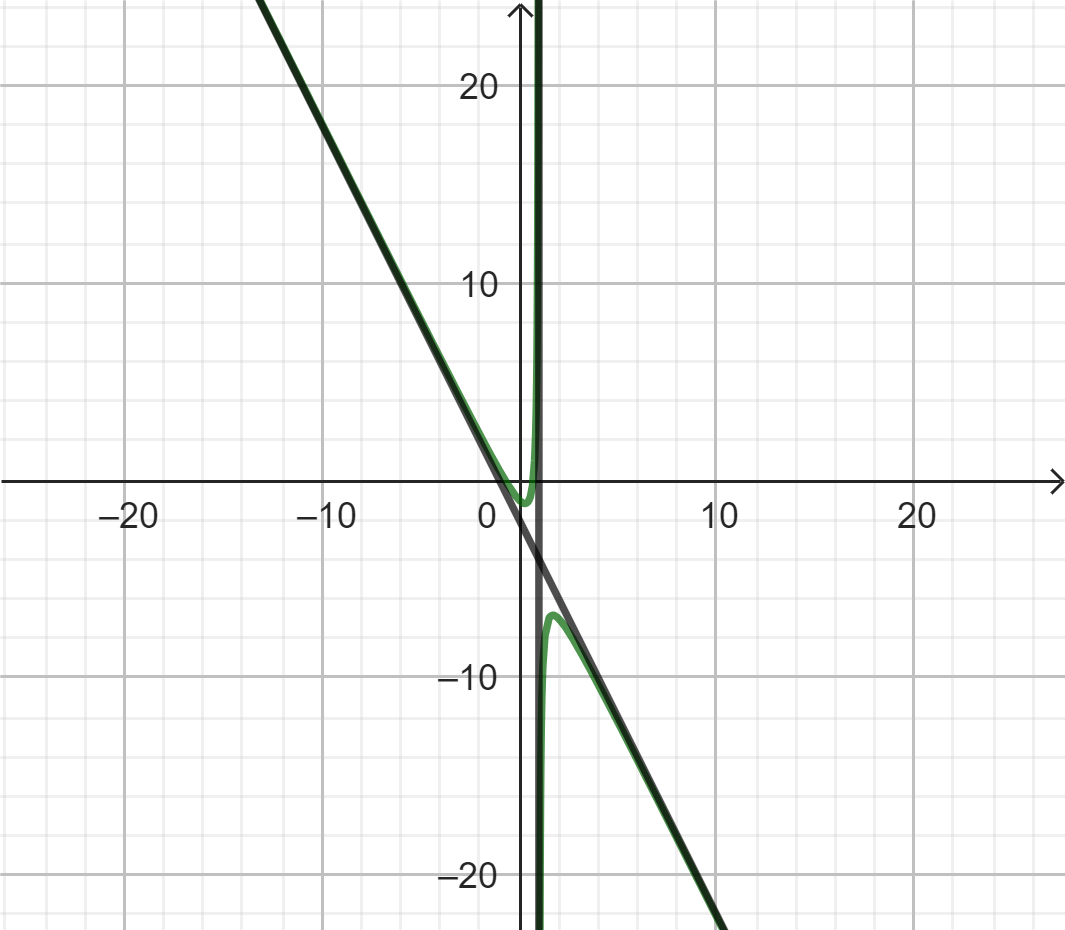
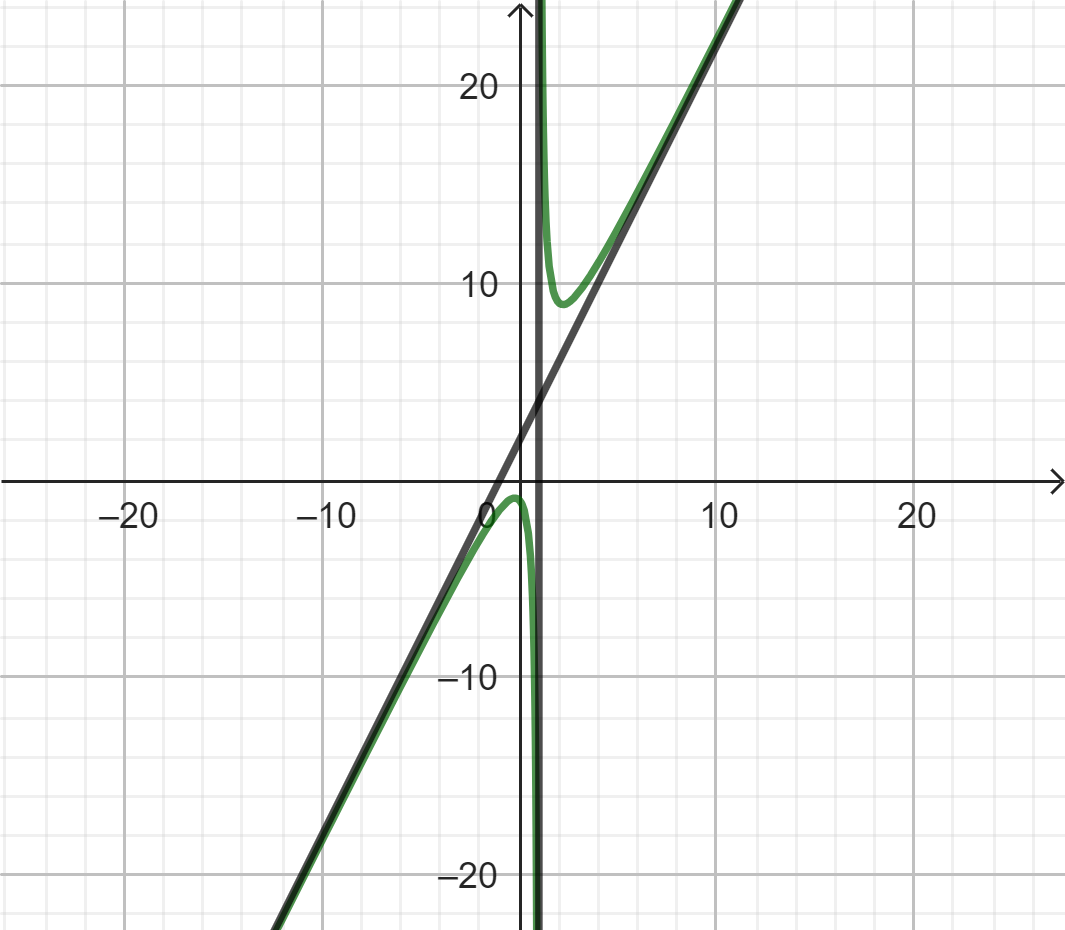
3.2. Dạng $y=\frac{ax^2+bx+c}{dx+e}.$

• Có tiệm cận đứng ($x=\frac{-e}{d}$) và tiệm cận xiên ($y=\dfrac{a}{d}x+\dfrac{b-\dfrac{ae}{d}}{d}$).

• Có tâm đối xứng là giao của 2 tiệm cận.

• Nhận hai đường phân giác của các góc tạo bởi 2 đường tiệm cận làm trục đối xứng.

| || |—|—|

B. Các dạng bài tập thường gặp

Dạng 1. Khảo sát hàm số bậc ba

Phương pháp:

Cho hàm số $y = ax^3 + bx^2 + cx + d$ $(a \neq 0)$

Bước 1: Tập xác định: $D = \mathbb{R}$

Bước 2: Khảo sát sự biến thiên của hàm số

• Giới hạn:
  • Với $a > 0$ thì $\lim_{x \to +\infty} y = +\infty$ và $\lim_{x \to -\infty} y = -\infty$
  • Với $a < 0$ thì $\lim_{x \to +\infty} y = -\infty$ và $\lim_{x \to -\infty} y = +\infty$

• Đạo hàm và cực trị:

  • $y’ = 3ax^2 + 2bx + c$

  • Hàm số có hai điểm cực trị khi $y’ = 0$ có hai nghiệm phân biệt $\Leftrightarrow \Delta’ > 0$

  • Gọi $A(x_1; y_1); B(x_2; y_2)$ là hai điểm cực trị, theo định lý Viet: \(\begin{cases} x_1 + x_2 = -\frac{2b}{3a} \\\\ x_1x_2 = \frac{c}{3a} \end{cases}\)
  • Hàm số không có cực trị khi $y’ = 0$ vô nghiệm hoặc nghiệm kép $\Leftrightarrow \Delta’ \leq 0$

• Bảng biến thiên: (Xem lại lý thuyết)

• Đồ thị hàm số:
  • Không có tiệm cận
  • Tâm đối xứng là điểm có hoành độ thỏa mãn $y’’ = 0 \Leftrightarrow x = -\frac{b}{3a}$

Ví dụ 1.1.

Khảo sát sự biến thiên và vẽ đồ thị của hàm số $y = f(x) = -x^3 + 3x^2 - 4$

Ví dụ 1.2.

Cho hàm số $y = ax^3 + bx^2 + cx + d$ có đồ thị như hình vẽ bên dưới. Hãy xác định dấu của các hệ số $a$, $b$, $c$ và $d$.

Dạng 2. Khảo sát hàm số hữu tỉ bậc nhất trên bậc nhất

Phương pháp:

Cho hàm số $y = \dfrac{ax + b}{cx + d}$ $(c \neq 0)$

Bước 1: Tập xác định: $D = \mathbb{R} \setminus \left\{-\frac{d}{c}\right\}$

Bước 2: Khảo sát sự biến thiên của hàm số

• Giới hạn và đường tiệm cận:

  • Tiệm cận ngang: $\lim\limits_{x \to \pm \infty} y = \frac{a}{c}$

    • Vậy $y = \frac{a}{c}$ là tiệm cận ngang của đồ thị hàm số

  • Tiệm cận đứng:

    • $\lim\limits_{x \to \left(-\frac{d}{c}\right)^-} y = +\infty$ và $\lim\limits_{x \to \left(-\frac{d}{c}\right)^+} y = -\infty$ hoặc: $\lim\limits_{x \to \left(-\frac{d}{c}\right)^-} y = -\infty$ và $\lim\limits_{x \to \left(-\frac{d}{c}\right)^+} y = +\infty$

    • Vậy $x = -\frac{d}{c}$ là tiệm cận đứng của đồ thị hàm số

• Đạo hàm: $y’ = \frac{ad - bc}{(cx + d)^2}$

  • Nếu $ad - bc > 0, \forall x \in D$: Hàm số đồng biến trên các khoảng $(-\infty; -\frac{d}{c})$ và $(-\frac{d}{c}; +\infty)$

  • Nếu $ad - bc < 0, \forall x \in D$: Hàm số nghịch biến trên các khoảng $(-\infty; -\frac{d}{c})$ và $(-\frac{d}{c}; +\infty)$

• Bảng biến thiên: (Xem lại lý thuyết)

• Đồ thị hàm số:

  • Đồ thị luôn có giao điểm của hai đường tiệm cận làm tâm đối xứng
  • Tâm đối xứng của đồ thị hàm số là $I\left(-\frac{d}{c}; \frac{a}{c}\right)$

Ví dụ 2.1.

Khảo sát sự biến thiên và vẽ đồ thị của hàm số

a) $y = \dfrac{x}{x+1}$

b) $y = \dfrac{2x+1}{x+1}$

Dạng 3. Khảo sát hàm số hữu tỉ bậc hai trên bậc nhất

Phương pháp:

Cho hàm số $y = \frac{ax^2 + bx + c}{dx + e}$ với $ad \neq 0$, $x \neq -\frac{e}{d}$ và tử số, mẫu số không có nghiệm chung.

Đưa về dạng: $y = \alpha x + \beta + \frac{\gamma}{dx + e}$ (chia đa thức)

Bước 1: Tập xác định: $D = \mathbb{R} \setminus \left\{-\frac{e}{d}\right\}$

Bước 2: Khảo sát sự biến thiên của hàm số

• Giới hạn và đường tiệm cận:
  • Tiệm cận đứng: $\lim\limits_{x \to \left(-\frac{e}{d}\right)^\pm} y = \pm\infty \Rightarrow x = -\frac{e}{d}$ là tiệm cận đứng
  • Tiệm cận xiên: $\lim\limits_{x \to \pm\infty} [y - (\alpha x + \beta)] = 0 \Rightarrow y = \alpha x + \beta$ là tiệm cận xiên
• Đạo hàm $y’$: $y’ = \frac{\alpha(dx + e)^2 - \gamma d}{(dx + e)^2}$
  • Dấu của $y’$ phụ thuộc vào dấu của $g(x) = \alpha(dx + e)^2 - \gamma d$
• Điều kiện có cực trị:
  • Nếu phương trình $y’ = 0$ vô nghiệm hoặc có nghiệm kép thì không có cực trị
  • Nếu phương trình $y’ = 0$ có hai nghiệm phân biệt thì có hai cực trị

• Bảng biến thiên

• Đồ thị hàm số:
  • Tìm giao điểm của đồ thị với các trục tọa độ (nếu có)
  • Đồ thị hàm số có giao điểm $I$ của hai đường tiệm cận làm tâm đối xứng

Nhận xét:

• Đồ thị hàm số có giao điểm của hai đường tiệm cận làm tâm đối xứng
• Hàm số có cực đại và cực tiểu khi và chỉ khi $y’ = 0$ có hai nghiệm phân biệt khác $-\frac{e}{d}$
• Trong trường hợp đồ thị có cực đại và cực tiểu, phương trình đường thẳng đi qua hai điểm cực trị là $y = \frac{2ax + b}{d}$
• Mọi tiếp tuyến tại điểm $M \in (C)$ cắt hai đường tiệm cận tại $A, B$ thì $M$ là trung điểm của $AB$
• Diện tích tam giác $IAB$ (với $I$ là giao điểm của hai tiệm cận) là hằng số
• Với mọi điểm $M \in (C)$, tích khoảng cách từ $M$ đến hai đường tiệm cận là hằng số
• Nếu từ điểm $E$ nằm trên một trong hai đường tiệm cận của $(C)$, chỉ vẽ được một tiếp tuyến duy nhất đến $(C)$ qua $E$

Ví dụ 3.1.

Khảo sát sự biến thiên và vẽ đồ thị của hàm số $y = \dfrac{2x^2 + 5x + 4}{x + 2}$ (H)

Ví dụ 3.2.

Khảo sát sự biến thiên và vẽ đồ thị của hàm số $y = \dfrac{x^2 + x - 2}{x + 1}$

Dạng 4. Nhận dạng hàm số khi biết đồ thị - bảng biến thiên.

Ví dụ 4.1.

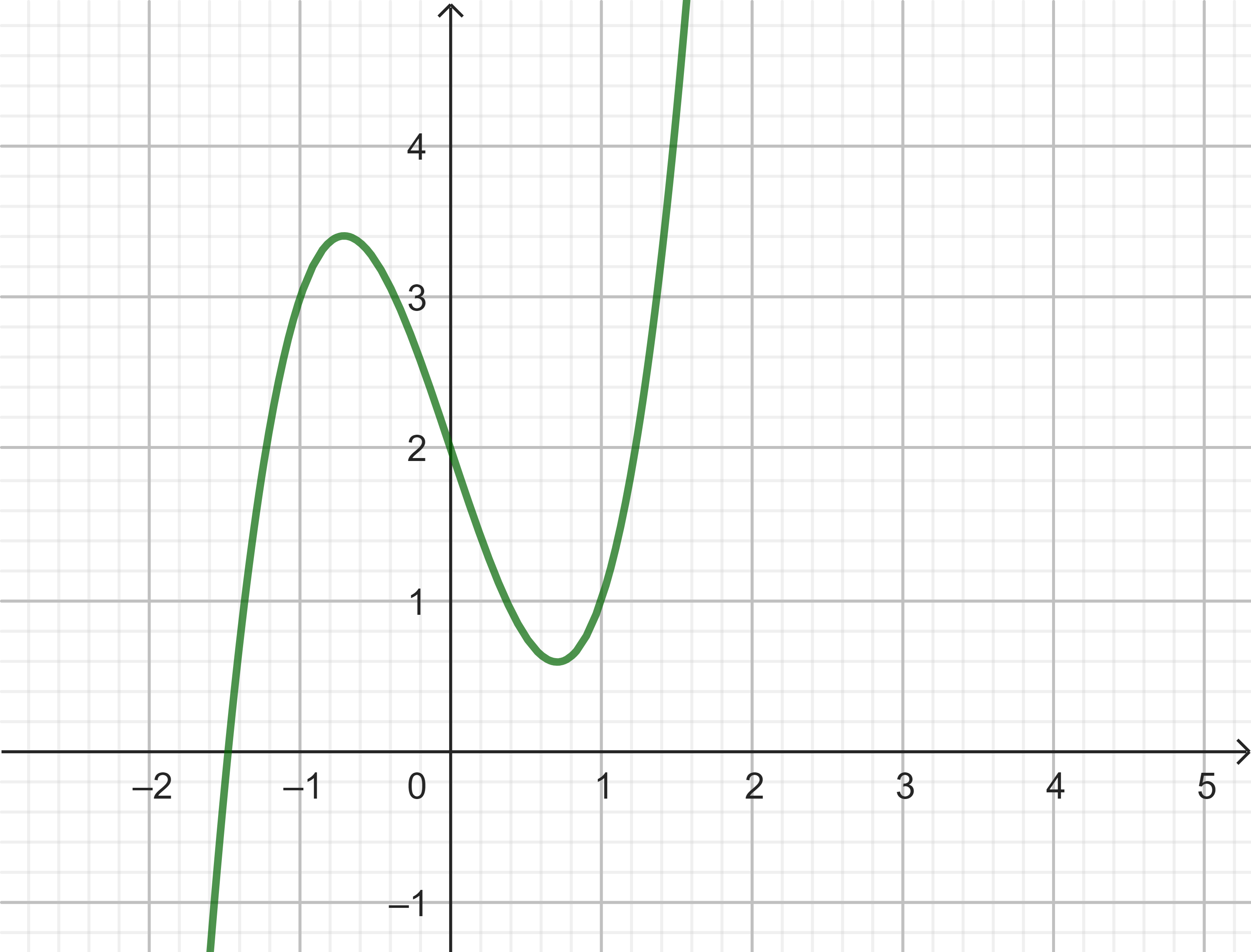
Cho hàm số bậc ba $y=f(x)$ có đồ thị như hình bên dưới. Viết công thức của hàm số.

Ví dụ 4.2.

Cho hàm số $y=\dfrac{ax-1}{2x+b}$ có bảng biến thiên như hình bên dưới. Xác định $a$ và $b$.

$x$	$-\infty$	$\,$	$-1$	$\,$	$+\infty$
$y’$	$\,$	$-$	$||$	$-$	$\,$
$y$	$-1$	$\searrow -\infty$	$||$	$+\infty\searrow$	$-1$

Ví dụ 4.3.

Cho hàm số hữu tỉ $y=\dfrac{2x^2+ax+b}{cx-2}$ có đồ thị như hình bên dưới. Viết công thức của hàm số.

Dạng 5. Nhận dạng đồ thị - bảng biến thiên khi biết hàm số

Phương pháp

Vận dụng các kiến thức liên quan: Đơn điệu, Cực trị, Đường tiệm cận

Bước 1: Tập xác định.

** Bước 2:** Sự biến thiên

• Chiều biến thiên.

• Cực trị.

• Đường tiệm cận.

• Điểm đi qua.

** Bước 3:** Kết luận đồ thị

Ví dụ 5.1.

Xác định bảng biến thiên của hàm số: $y = -x^3 - 3x^2 + 9x - 9$

Ví dụ 5.2.

Xác định đồ thị của hàm số hữu tỉ: $y = \dfrac{x^2 + 3}{x + 1}$

Dạng 6. Xác định dấu – giá trị các hệ số

Phương pháp

Loại 1. Hàm đa thức bậc ba

Dạng hàm: $y = f(x) = ax^3 + bx^2 + cx + d$ ($a \neq 0$)

Bước 1: Nhìn vào nhánh ngoài cùng của đồ thị để xác định dấu của hệ số $a$.

Bước 2: Điểm cắt trục tung: xác định dấu hệ số $d$.

Bước 3: Nhìn vào hai điểm cực trị (nếu có) ta biết nghiệm của phương trình $y’ = 0$ tương đương với $3ax^2 + 2bx + c = 0$.

• Nếu đồ thị hàm số không có điểm cực trị: $\Delta’ = b^2 - 3ac \leq 0.$

• Nếu đồ thị hàm số có hai điểm cực trị:

  • Các điểm cực trị $x_1, x_2$ của hàm số là hai nghiệm của phương trình $y’ = 0$

  • Khi đó:

    • $x_1 + x_2 = -\dfrac{2b}{3a}$ và $x_1x_2 = \dfrac{c}{3a}$ (công thức Vi-ét)

    • Dựa vào vị trí của $x_1, x_2$ để suy luận các phép tính $x_1 + x_2$ và $x_1x_2$ mang dấu gì.

    • Nếu không cho tọa độ rõ ràng, ước lượng khoảng cách từ O tới các điểm $x_1, x_2$.

Bước 4: Xác định tọa độ các điểm đã cho.

Bước 5: Dựa vào điểm uốn:

• Là tâm đối xứng của đồ thị hàm số.

• $x_u$ là nghiệm của phương trình $y^{\prime\prime} = 0$.

• Điểm uốn là trung điểm của đoạn thẳng nối hai điểm cực trị.

Nhận xét:

• Bảng biến thiên mô phỏng đồ thị hàm số

• Cách đọc bảng biến thiên giống như cách đọc đồ thị

Loại 2. Hàm phân thức

Dạng hàm: $y = \dfrac{ax + b}{cx + d}$ và $y = \dfrac{ax^2 + bx + c}{dx + e}$

Bước 1: Xác định các đường tiệm cận:

• Dùng công thức tính nhanh (định nghĩa) để tìm mối quan hệ giữa các hệ số.

• Lưu ý: Giao điểm của hai đường tiệm cận là tâm đối xứng của đồ thị hàm số

Bước 2: Xác định các điểm thuộc đồ thị hàm số: giao với các trục tọa độ, cực trị.

Bước 3: Từ hình dáng đồ thị (bảng biến thiên), xác định dấu của đạo hàm dựa vào các khoảng đồng biến/nghịch biến. Từ đó xác định dấu của các hệ số.

Ví dụ 6.1.

Cho hàm số bậc ba $y = ax^3 + bx^2 + cx + d$ có đồ thị như hình vẽ. Trong các hệ số $a, b, c, d$, có bao nhiêu giá trị dương?

Ví dụ 6.2.

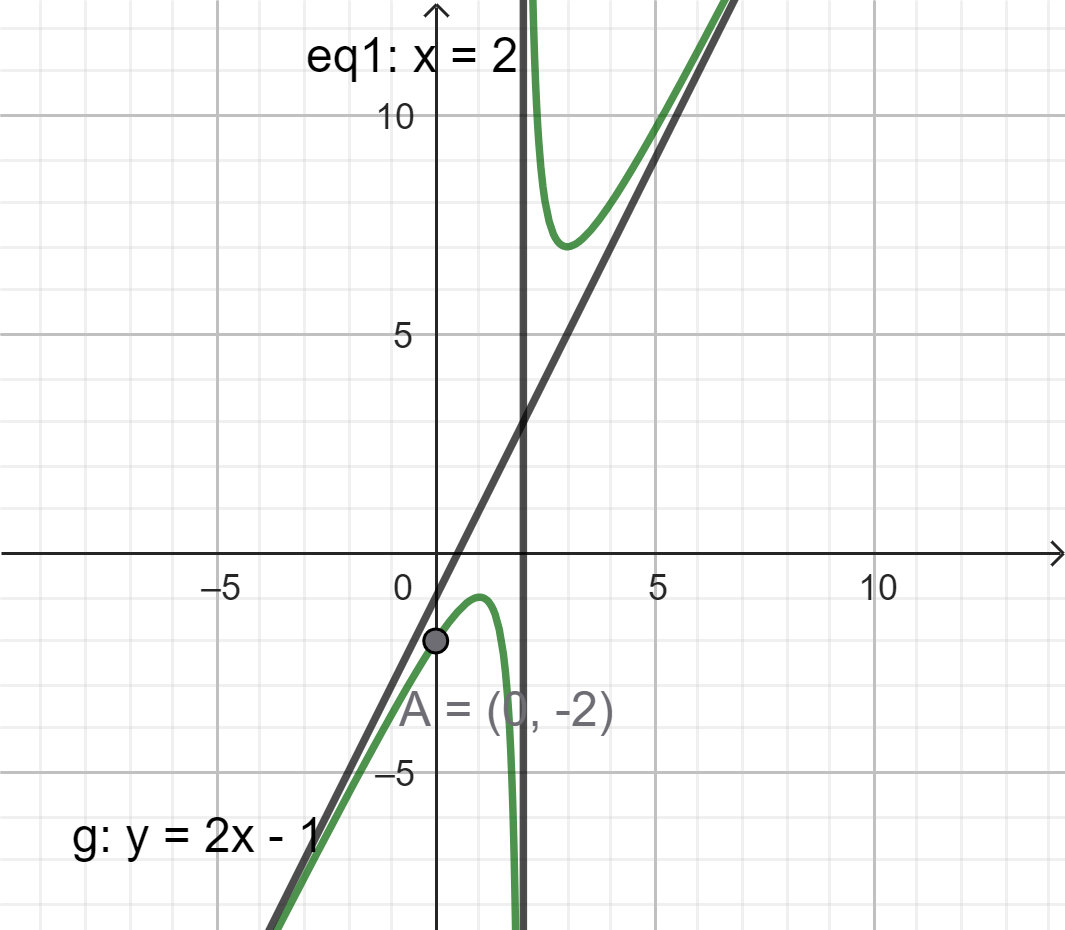
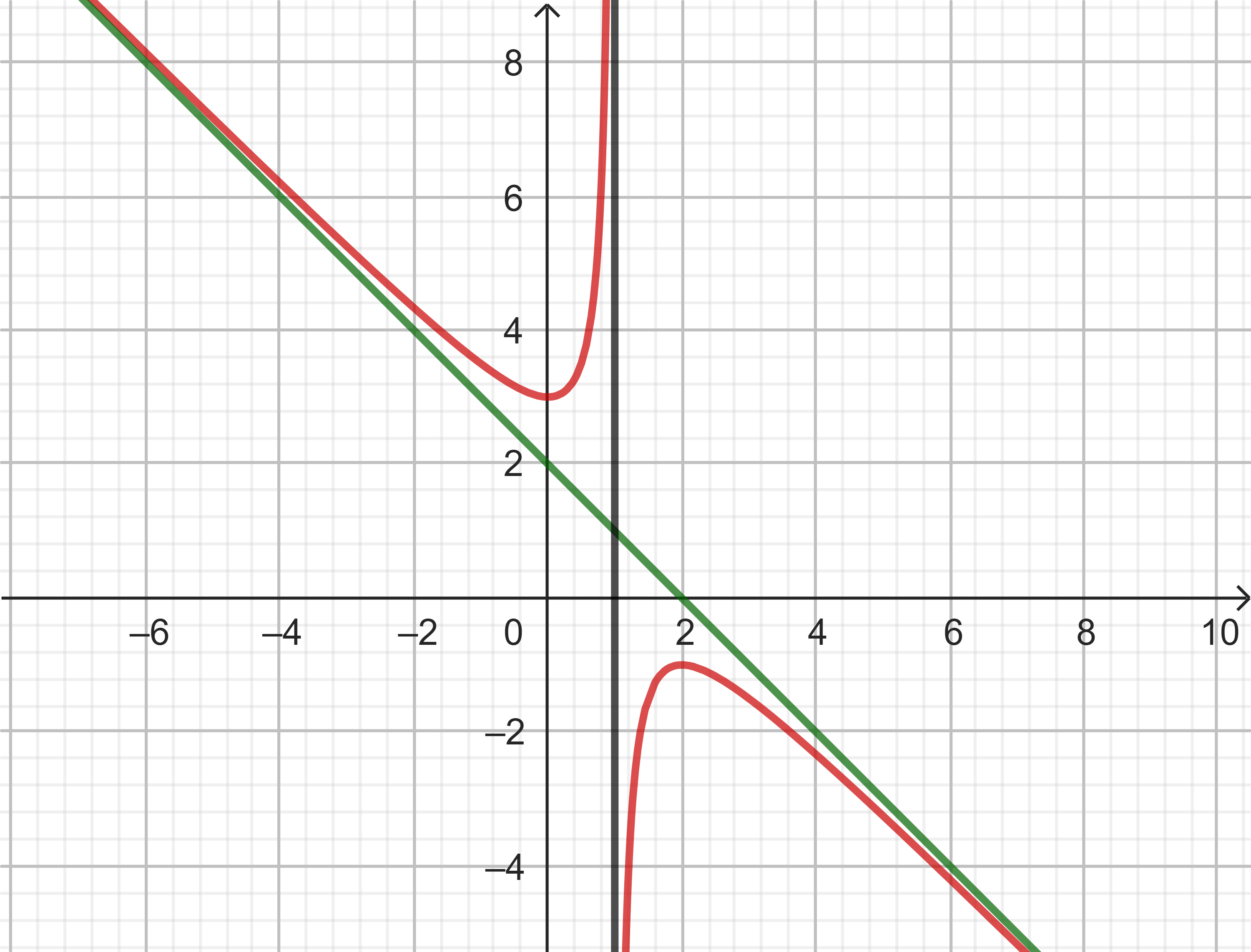
Cho hàm số hữu tỉ $y = ax + 2 + \dfrac{b}{x+c}$ có đồ thị như hình bên. Tính $P = a + b + c$.

Dạng 7. Đọc đồ thị của đạo hàm

Phương pháp

Để xác định tính đơn điệu, cực trị, giá trị min/max của hàm số $y = f(x)$, $g(x) = f(u(x))$ hoặc $g(x) = g(f(x))$ khi cho đồ thị (hoặc bảng biến thiên) của đạo hàm $y = f^\prime (x)$ hoặc $y = f^\prime (u(x))$.

Bước 1: Tính $g’(x)$

• Lưu ý: Nếu $g(x) = f(u(x))$ thì $g’(x) = u’(x) \cdot f^\prime(u(x))$

Bước 2: Giải $g’(x) = 0$ để tìm các điểm tới hạn $x_1, x_2, …, x_n$ hoặc các điểm mà $g’(x)$ không xác định.

Bước 3: Lập bảng xét dấu của $g’(x)$. Từ đó lập bảng biến thiên của hàm số $y = g(x)$. Cuối cùng sử dụng bảng biến thiên để xác định các tính chất như tính đơn điệu, cực trị (cực tiểu/cực đại cục bộ), giá trị min/max.

Ví dụ 7.1.

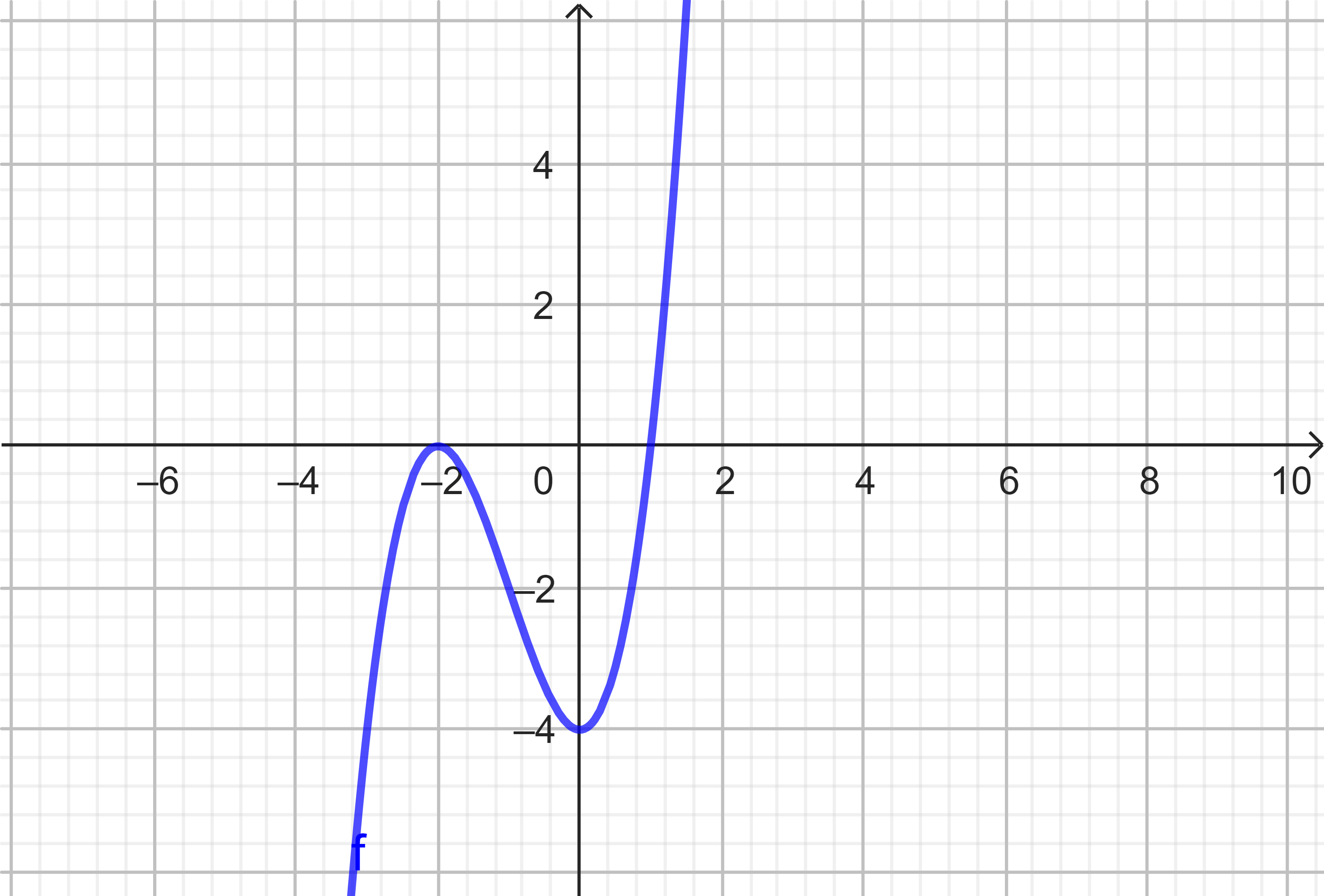
Cho hàm số $y = f(x)$ liên tục trên $\mathbb{R}$, $y = f’(x)$ có đồ thị trong hình dưới đây. Lập bảng xét dấu của $y = f’(x)$?

Ví dụ 7.2.

Cho hàm số $y = f(x)$ liên tục trên $\mathbb{R}$, $y = f’(x)$ có đồ thị dưới đây. Tìm điểm cực đại của hàm số đã cho.

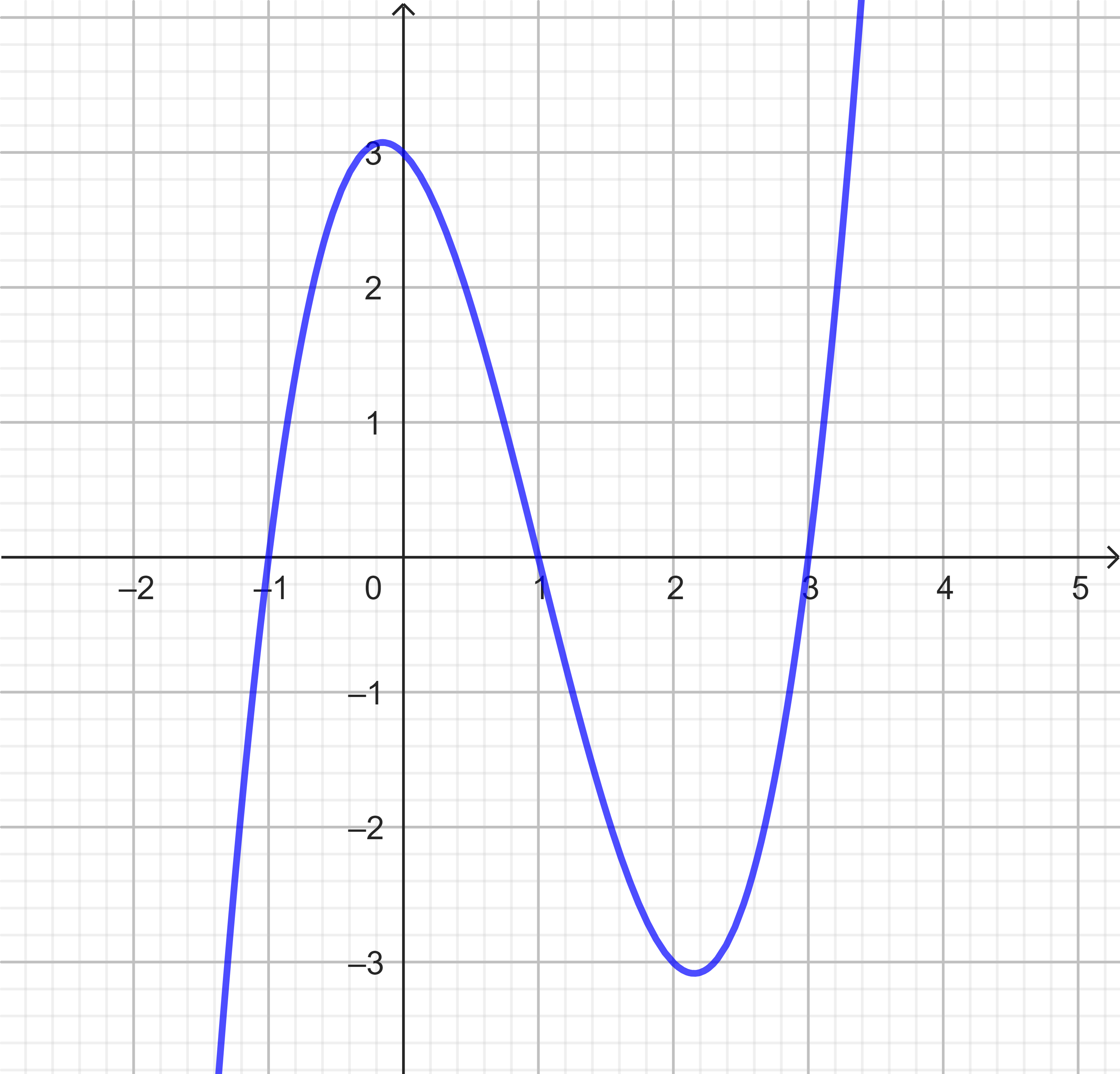
Ví dụ 7.3.

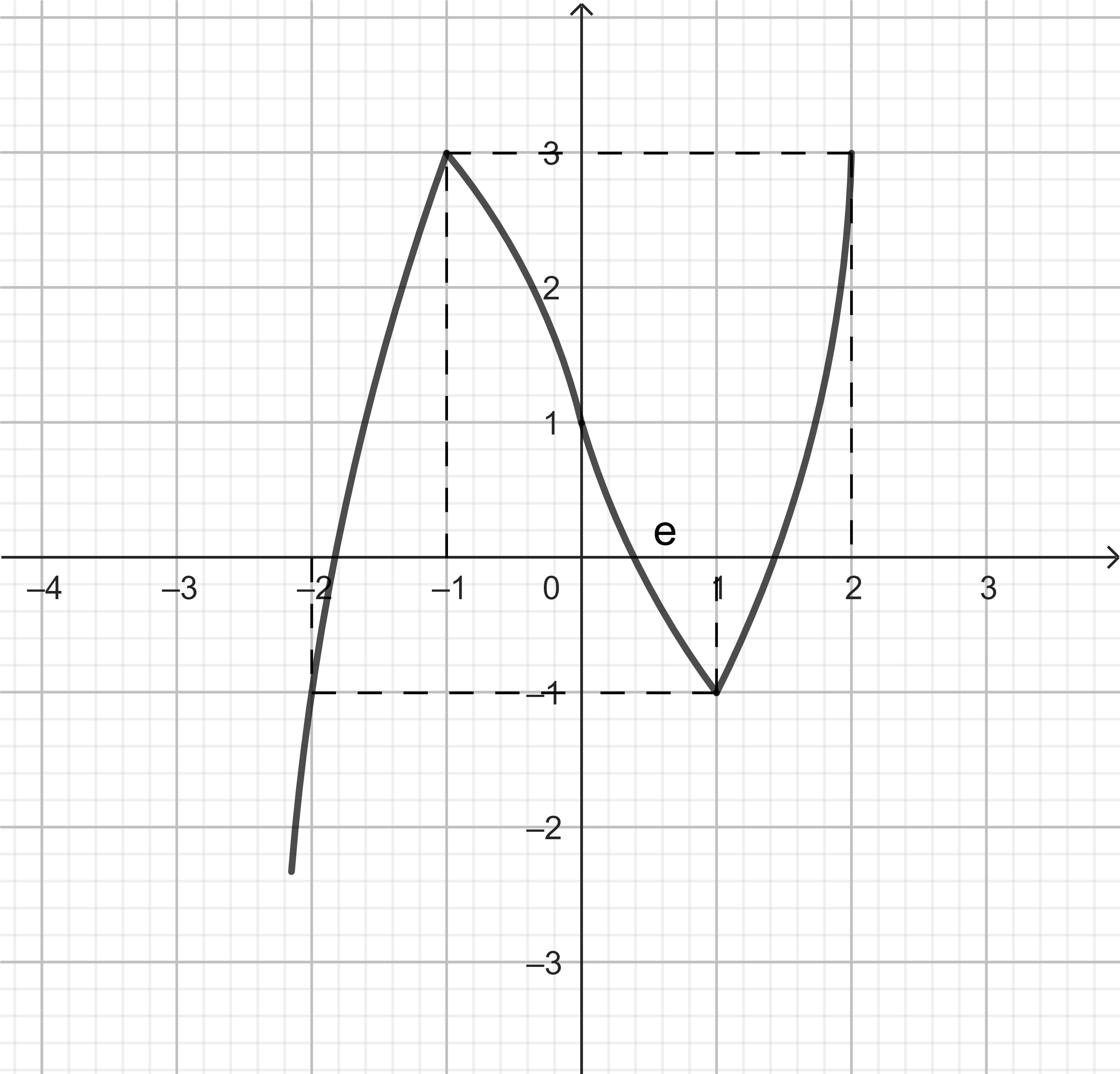
Cho hàm số $f(x)$ có đạo hàm trên $\mathbb{R}$ và hàm số $y = f’(x)$ có đồ thị như hình vẽ. Xác định giá trị lớn nhất của hàm số $g(x) = f(2x-1) - 2x + 1$ trên $[0;1]$.

Dạng 8. Sự tương giao

Phương pháp:

Các hàm số $y = f(x)$, $y = g(x)$ có đồ thị lần lượt là các đường $(C_1)$, $(C_2)$, khi đó:

• Số nghiệm của phương trình $f(x) = g(x)$ chính là số giao điểm của các đồ thị $(C_1)$, $(C_2)$.

• Số giao điểm của các đường $(C_1)$, $(C_2)$ chính là số nghiệm của phương trình $f(x) = g(x)$.

Ví dụ 8.1.

Có bao nhiêu giá trị nguyên dương của tham số $m$ để đồ thị của hàm số $y = 3x^3 - 9x + 3(m-1)$ giao với trục hoành tại hai điểm phân biệt?

Ví dụ 8.2.

Có tất cả bao nhiêu giá trị thực của tham số $m$ để đồ thị của hàm số $y = x^3 - 3x^2 + (2m^2 + 1)x + m - 3$ và parabol $y = 2x^2 + x - m - 2$ có hai giao điểm phân biệt và tổng hoành độ hai giao điểm đó là $3$?

Dạng 9. Bài toán thực tế liên môn đưa về khảo sát hàm số

Phương pháp

Bước 1: Xác định yếu tố chọn làm ẩn, chỉ ra điều kiện (nếu có).

Bước 2: Xây dựng phương trình hàm số từ các dữ kiện của bài toán.

Bước 3: Giải bài toán liên quan đến hàm số và kết luận.

Ví dụ 9.1.

Nhiệt độ $T$ của một người trong cơn bệnh được cho bởi công thức $T(t) = -0,1t^2 + 1,2t + 98,6$ $(0 \leq t \leq 11)$, trong đó $T$ là nhiệt độ (°F – Fahrenheit) theo thời gian $t$ trong ngày. Biết rằng $°C = \dfrac{°F - 32}{1,8}$. Hỏi độ chênh lệch (theo độ $°C$) giữa nhiệt độ lớn nhất và nhiệt độ thấp nhất trong một ngày là bao nhiêu?

Ví dụ 9.2.

Một sợi dây kim loại dài 60 cm được cắt thành hai đoạn. Đoạn dây thứ nhất uốn thành hình vuông cạnh $a$, đoạn dây thứ hai uốn thành đường tròn bán kính $r$. Để tổng diện tích của hình vuông và hình tròn là nhỏ nhất thì tỉ số $\dfrac{a}{r}$ bằng bao nhiêu?

Ví dụ 9.3.

Một cơ sở sản xuất khăn mặt có giá bán hiện tại là 30.000 đồng/chiếc, bán được trung bình 3.000 chiếc/tháng. Chi phí sản xuất cố định là 18.000 đồng/chiếc. Qua nghiên cứu thị trường, người ta thấy rằng cứ tăng giá 1.000 đồng thì số lượng bán giảm 100 chiếc/tháng. Hỏi cơ sở nên bán với giá bao nhiêu để có lợi nhuận cao nhất?