Chương 03: CÁC SỐ ĐO ĐẶC TRƯNG CỦA MẪU SỐ LIỆU GHÉP NHÓM
Bài 1. KHOẢNG BIẾN THIÊN - KHOẢNG TỨ PHÂN VỊ CỦA MẪU SỐ LIỆU GHÉP NHÓM
A. Lý thuyết
1. Khoảng biến thiên
Định nghĩa:
Khoảng biến thiên của mẫu số liệu ghép nhóm, kí hiệu là $R$, là hiệu số giữa đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên.
Xét mẫu số liệu ghép nhóm được cho ở bảng sau:
| Nhóm | $[u_1; u_2)$ | $[u_2; u_3)$ | ... | $[u_k; u_{k+1})$ |
|---|---|---|---|---|
| Tần số | $n_1$ | $n_2$ | ... | $n_k$ |
Nếu $n_1$ và $n_k$ đều khác 0 thì:
$$R = u_{k+1} - u_1$$
Ý nghĩa:
- Khoảng biến thiên của mẫu số liệu ghép nhóm luôn lớn hơn hoặc bằng khoảng biến thiên của mẫu số liệu gốc.
- Khoảng biến thiên của mẫu số liệu ghép nhóm là giá trị xấp xỉ cho khoảng biến thiên của mẫu số liệu gốc và có thể dùng để đo mức độ phân tán của mẫu số liệu.
- Khoảng biến thiên $R = u_{k+1} - u_1$ chưa phản ánh được đầy đủ mức độ phân tán của phần lớn các số liệu.
- Hơn nữa, giá trị của R thường tăng vọt khi xuất hiện giá trị ngoại lệ trong mẫu số liệu. Do đó, để phản ánh mức độ phân tán của số liệu, người ta còn dùng các số đặc trưng khác.
2. Khoảng tứ phân vị
Định nghĩa:
Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu là $\Delta_Q$, là hiệu giữa tứ phân vị thứ ba $Q_3$ và tứ phân vị thứ nhất $Q_1$ của mẫu số liệu ghép nhóm đó, tức là:
$$\Delta_Q = Q_3 - Q_1$$
Ý nghĩa:
- Khoảng tứ phân vị đo lường mức độ phân tán của 50% số liệu chính giữa của mẫu số liệu.
- Khoảng tứ phân vị của mẫu số liệu ghép nhóm càng nhỏ thì dữ liệu càng tập trung xung quanh trung vị.
- Khoảng tứ phân vị được dùng để xác định giá trị ngoại lệ trong mẫu số liệu. Giá trị $x$ trong mẫu số liệu là giá trị ngoại lệ nếu $x > Q_3 + 1,5\Delta_Q$ hoặc $x < Q_1 - 1,5\Delta_Q$.
- Khoảng tứ phân vị không bị ảnh hưởng nhiều bởi các giá trị ngoại lệ.
Công thức xác định tứ phân vị:
Tứ phân vị thứ $i$ ($i \in \{1, 2, 3\}$), kí hiệu là $Q_i$, của mẫu số liệu ghép nhóm được xác định như sau:
$$Q_i = u_m + \frac{\frac{in}{4} - C}{n_m}(u_{m+1} - u_m)$$
Trong đó:
- $n = n_1 + n_2 + ... + n_k$ là cỡ mẫu.
- $[u_m; u_{m+1})$ là nhóm chứa tứ phân vị thứ $i$.
- $n_m$ là tần số của nhóm chứa tứ phân vị thứ $i$.
- $C = n_1 + n_2 + ... + n_{m-1}$ là tần số tích lũy của nhóm trước nhóm chứa tứ phân vị thứ $i$.
B. Các dạng bài tập
Dạng 1. Khoảng biến thiên của MSL ghép nhóm
Phương pháp:
Để tìm khoảng biến thiên $R$ của mẫu số liệu ghép nhóm, ta lấy đầu mút phải của nhóm cuối cùng trừ đi đầu mút trái của nhóm đầu tiên: $R = u_{k+1} - u_1$.
Ví dụ 1.1.
Dữ liệu về tốc độ của 100 xe ô tô lưu thông trên một đoạn đường cao tốc vào giờ cao điểm được cho trong bảng sau. Hãy tìm khoảng biến thiên của mẫu số liệu.
| Tốc độ (km/h) | $[60;70)$ | $[70;80)$ | $[80;90)$ | $[90;100)$ | $[100;110)$ |
|---|---|---|---|---|---|
| Số xe | 10 | 20 | 20 | 35 | 15 |
Ví dụ 1.2.
Thời gian hoàn thành bài kiểm tra của các bạn trong lớp 12A được cho trong bảng sau:
| Thời gian (phút) | $[25;30)$ | $[30;35)$ | $[35;40)$ | $[40;45)$ |
|---|---|---|---|---|
| Số học sinh | 8 | 16 | 4 | 2 |
- Tính khoảng biến thiên R cho mẫu số liệu ghép nhóm trên.
- Nếu biết học sinh hoàn thành bài kiểm tra sớm nhất mất 27 phút và muộn nhất mất 43 phút. Hãy so sánh khoảng biến thiên của mẫu số liệu ghép nhóm và mẫu số liệu gốc.
Dạng 2. Ý nghĩa của khoảng biến thiên trong việc đo mức độ phân tán
Phương pháp:
- Khoảng biến thiên là một thước đo sơ bộ về sự phân tán của dữ liệu.
- Giá trị R càng lớn, dữ liệu càng phân tán.
- Tuy nhiên, R rất nhạy với các giá trị ngoại lệ và có thể không phản ánh đúng sự phân tán của phần lớn dữ liệu.
Ví dụ 2.1.
Để chuẩn bị mở một trung tâm thể dục thể thao, anh Sơn đã tiến hành điều tra tuổi thọ của máy chạy bộ (đơn vị: năm) do hai hãng X, Y sản xuất. Bảng số liệu thu thập được như sau:
| Tuổi thọ (năm) | $[2;4)$ | $[4;6)$ | $[6;8)$ | $[8;10)$ | $[10;12)$ |
|---|---|---|---|---|---|
| Số máy của hãng X | 7 | 20 | 36 | 20 | 17 |
| Số máy của hãng Y | 0 | 20 | 35 | 35 | 10 |
Khoảng biến thiên của mẫu số liệu nào lớn hơn? Từ đó có thể nói là máy chạy bộ do hãng nào sản xuất có tuổi thọ phân tán hơn?
Ví dụ 2.2.
Người ta tiến hành phỏng vấn hai nhóm khán giả về một bộ phim mới công chiếu theo thang điểm 100. Bảng dưới đây trình bày kết quả điều tra hai nhóm khán giả:
| Điểm | $[2;4)$ | $[4;6)$ | $[6;8)$ | $[8;10)$ | $[10;12)$ |
|---|---|---|---|---|---|
| Số người của nhóm A | 7 | 20 | 36 | 20 | 17 |
| Số người của nhóm B | 0 | 20 | 35 | 35 | 10 |
Ý kiến đánh giá của nhóm khán giả nào phân tán hơn?
Ví dụ 2.3.
Bảng dưới biểu thị kết quả điều tra thời gian sử dụng Internet hằng ngày của một số người.
| Thời gian (phút) | $[30;60)$ | $[60;90)$ | $[90;120)$ | $[120;150)$ | $[150;180]$ |
|---|---|---|---|---|---|
| Số người | 2 | 4 | 10 | 5 | 3 |
Tìm khoảng biến thiên của mẫu số liệu đã cho. Kết quả cho biết điều gì?
Dạng 3. Khoảng tứ phân vị của MSL ghép nhóm
Phương pháp:
- Bước 1: Xác định cỡ mẫu $n$.
- Bước 2: Xác định nhóm chứa $Q_1$. Đây là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng $\frac{n}{4}$. Áp dụng công thức để tính $Q_1$.
- Bước 3: Xác định nhóm chứa $Q_3$. Đây là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng $\frac{3n}{4}$. Áp dụng công thức để tính $Q_3$.
- Bước 4: Tính khoảng tứ phân vị: $\Delta_Q = Q_3 - Q_1$.
Ví dụ 3.1.
Một người ghi lại thời gian đàm thoại của một số cuộc gọi cho kết quả như bảng sau:
| Thời gian (phút) | $[0;1)$ | $[1;2)$ | $[2;3)$ | $[3;4)$ | $[4;5)$ |
|---|---|---|---|---|---|
| Số cuộc gọi | 8 | 20 | 25 | 17 | 10 |
Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm trên.
Ví dụ 3.2.
Bạn An rất thích chạy bộ. Thời gian chạy bộ mỗi ngày trong thời gian gần đây của bạn An được thống kê lại ở bảng sau:
| Thời gian (phút) | $[20;25)$ | $[25;30)$ | $[30;35)$ | $[35;40)$ | $[40;45)$ |
|---|---|---|---|---|---|
| Số ngày | 6 | 6 | 4 | 1 | 1 |
Hãy tính khoảng tứ phân vị của mẫu số liệu ghép nhóm trong bảng trên.
Ví dụ 3.3.
Khảo sát năng suất của một số thửa ruộng được minh họa ở biểu đồ sau:
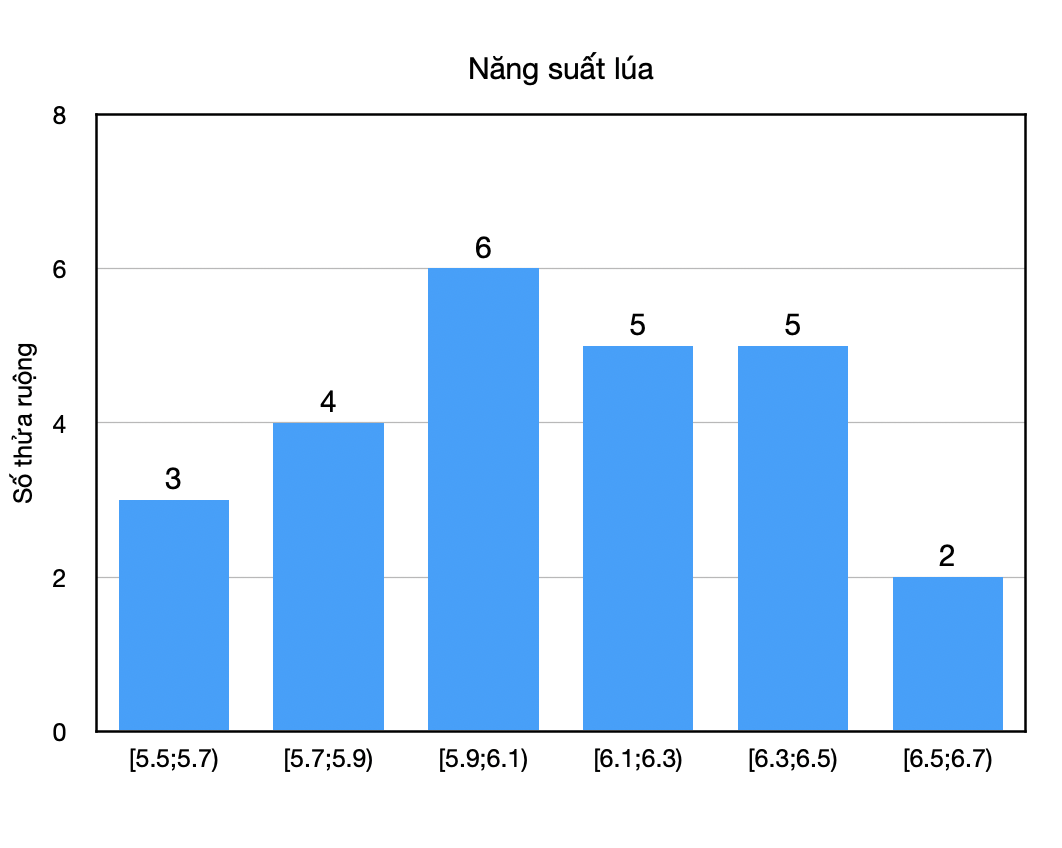
- Có bao nhiêu thửa ruộng được khảo sát?
- Lập bảng tần số ghép nhóm và tần số tương đối ghép nhóm tương ứng của mẫu số liệu trên.
- Hãy xác định khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu trên.
Dạng 4. Ý nghĩa của khoảng tứ phân vị trong việc đo mức độ phân tán
Phương pháp:
- Khoảng tứ phân vị $\Delta_Q$ cho biết mức độ phân tán của 50% dữ liệu nằm ở trung tâm.
- $\Delta_Q$ càng nhỏ, mức độ tập trung của dữ liệu quanh trung vị càng cao, dữ liệu càng "đều" hơn.
- Sử dụng $\Delta_Q$ để xác định các giá trị ngoại lệ (bất thường): một giá trị $x$ được coi là ngoại lệ nếu $x < Q_1 - 1,5\Delta_Q$ hoặc $x > Q_3 + 1,5\Delta_Q$.
Ví dụ 4.1.
Kết quả đo chiều cao của 100 cây dừa trồng sau 10 năm tại một vườn trái cây ở Bến Tre cho ở bảng sau:
| Chiều cao (m) | $[8,4;8,6)$ | $[8,6;8,8)$ | $[8,8;9,0)$ | $[9,0;9,2)$ | $[9,2;9,4)$ |
|---|---|---|---|---|---|
| Số cây | 5 | 12 | 25 | 44 | 14 |
- Hãy tìm khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm trên.
- Trong 100 cây dừa trên có 1 cây cao 8,4 m. Hỏi chiều cao của cây dừa này có phải là giá trị ngoại lệ không?
Ví dụ 4.2.
Biểu đồ sau mô tả kết quả điều tra về điểm trung bình năm học của học sinh hai trường A và B.
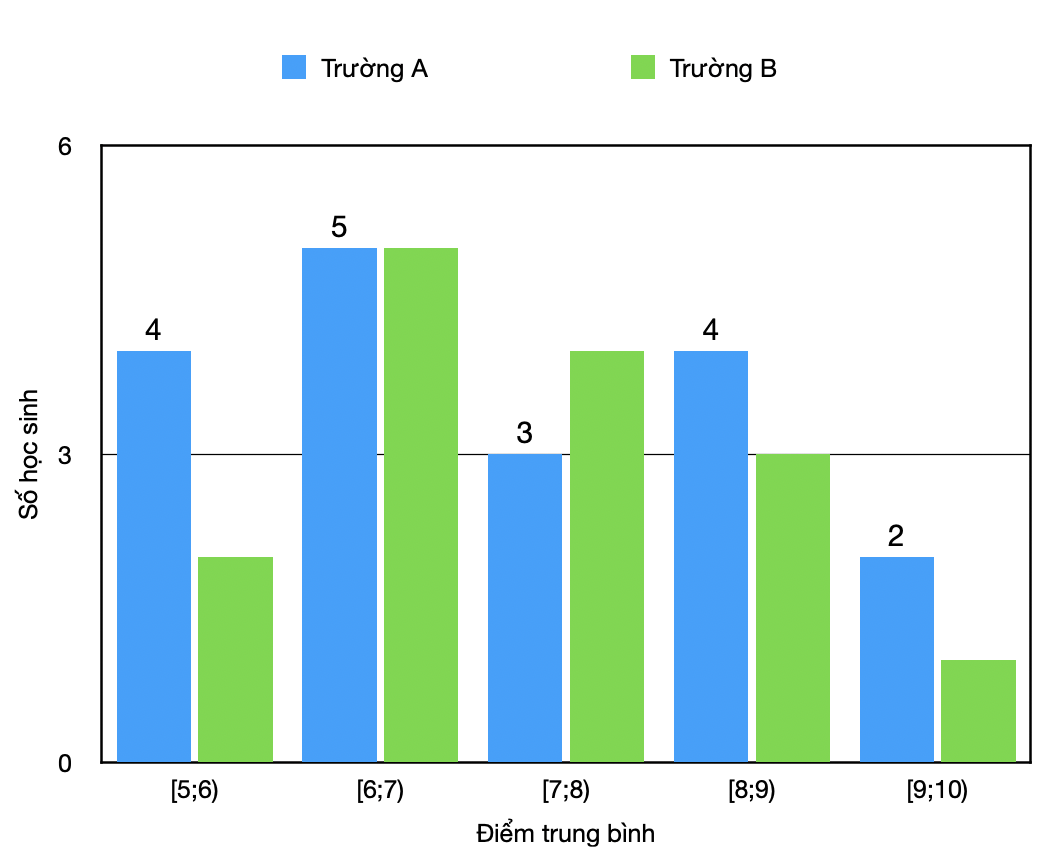
- Hãy xác định giá trị đại diện cho mỗi nhóm và lập bảng tần số ghép nhóm cho mẫu số liệu trên.
- Nếu so sánh theo khoảng tứ phân vị của mẫu số liệu ghép nhóm thì học sinh trường nào có điểm trung bình đều hơn?