Chương 1. Ứng dụng đạo hàm
Bài 1. Tính đơn điệu và cực trị của hàm số
Phần I: Câu hỏi trắc nghiệm (Mỗi câu hỏi yêu cầu học sinh chọn một phương án)
Câu 1
Cho hàm số $y = f(x)$ xác định với mọi $x \neq -4$ có bảng biến thiên như hình vẽ dưới đây. Hàm số đồng biến trên khoảng nào trong các khoảng sau?
Bảng biến thiên:
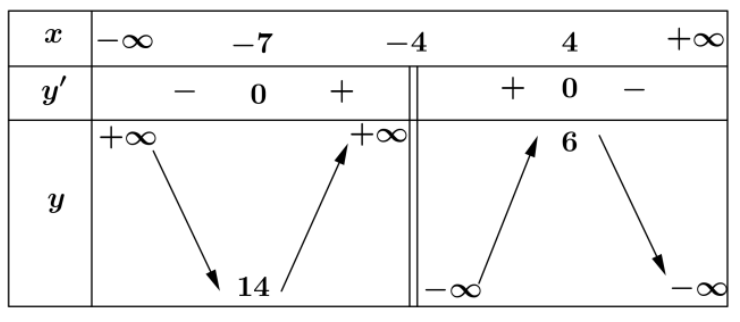
Các phương án:
- $(-7; + \infty)$
- $(-7; -4)$
- $(6; + \infty)$
- $(-7; 4)$
Câu 2
Cho hàm số $y = f(x)$ xác định trên $\mathbb{R}$ và có bảng biến thiên như hình vẽ sau.
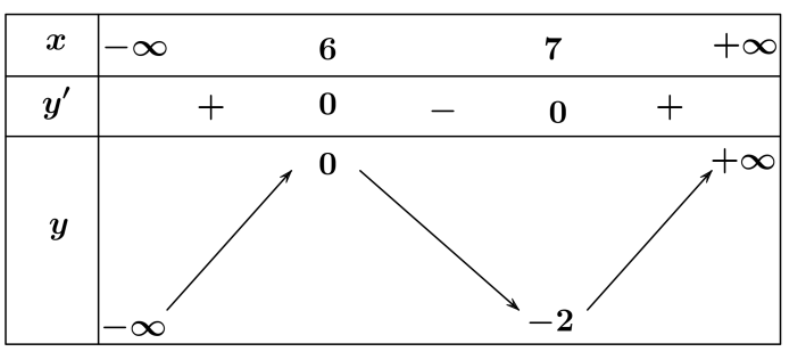 Tìm điểm cực đại của hàm số $y = f(x)$.
Tìm điểm cực đại của hàm số $y = f(x)$.
- $x = 7$
- $x = -2$
- $x = 0$
- $x = 6$
Câu 3
Hàm số $y = \sqrt[3]{x^2}$ có tất cả bao nhiêu điểm cực trị?
Các phương án:
- 0
- 1
- 2
- 3
Câu 4
Một vật có phương trình quãng đường tính theo thời gian là $s(t) = 5 + 8t - 2t^2$. Tại thời điểm nào, vật cách mốc tính quãng đường khoảng lớn nhất?
Các phương án:
- 1 giây
- 2 giây
- 3 giây
- 4 giây
Câu 5
Cho hàm số $y = -\frac{x^3}{3} + x^2 + 4$. Hàm số nghịch biến trên khoảng nào trong các khoảng sau đây?
- $(0; 2)$
- $(-\infty; 0)\cup (2; +\infty)$
- $(0; +\infty)$
- $(-\infty; 0)$
Câu 6
Cho hàm số $y = \frac{2x + 8}{5x - 9}$. Hàm số nghịch biến trên khoảng nào trong các khoảng sau?
- $(-\infty; 5)$
- $(-\infty; +\infty)$
- $(0; +\infty)$
- $(2; +\infty)$ ✓
Câu 7
Cho hàm số $y = \frac{-x^2 + 11x - 1}{x - 11}$. Hàm số nghịch biến trên khoảng nào trong các khoảng sau?
- $(-\infty; 11)$
- $(10; +\infty)$
- $(8; 15)$
- $(-\infty; 6)$
Câu 8
Cho hàm số $y = \frac{2x}{x^2 + 8}$. Hàm số nghịch biến trên khoảng nào trong các khoảng sau?
- $(-6; +\infty)$
- $(-2\sqrt{2}; +\infty)$
- $(-\infty; 7)$
- $(-\infty; -2\sqrt{2})$
Câu 9
Cho hàm số $y = f(x)$ là hàm số bậc ba có đồ thị là đường cong trong hình dưới đây. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
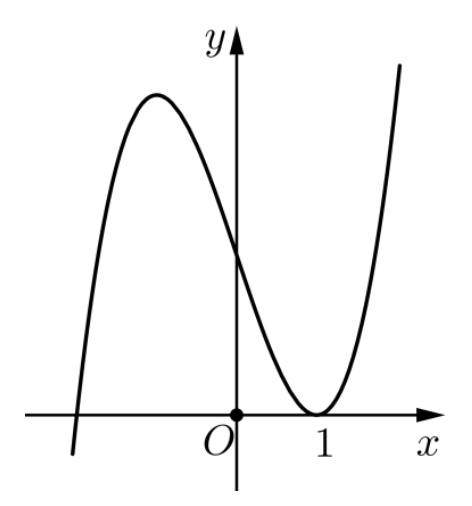
- $(1; +\infty)$
- $(0; 1)$
- $(-\infty; 2)$
- $(-\infty; 0)$
Câu 10
Một vật dao động có phương trình là $x(t) = 2\sin\left(\frac{\pi}{2}t - \frac{\pi}{3}\right)$ cm, $t$ có đơn vị là giây. Mệnh đề nào sau đây đúng? Trong khoảng 2 giây đến 3 giây, vận tốc của vật tăng hay giảm?
- Trong khoảng 2 giây đến 3 giây, vận tốc của vật không đổi.
- Trong khoảng 2 giây đến 3 giây, vận tốc của vật luôn tăng.
- Trong khoảng 2 giây đến 3 giây, vận tốc của vật luôn giảm.
- Trong khoảng 2 giây đến 3 giây, vận tốc của vật giảm, sau đó tăng.
Câu 11
Cho hàm số $y = \frac{2x^2 - 2x + 2}{x - 1}$. Giá trị cực tiểu của hàm số đã cho là
- 6
- -2
- 0
- 2
Câu 12
Cho hàm số $y = f(x) = x^3 - \frac{21x^2}{2} + 36x - 1$. Điểm cực tiểu của hàm số đã cho là
- $x = 8$
- $x = 4$
- $x = 1$
- $x = 3$
Phần II: Câu trắc nghiệm đúng sai
Câu 1
Cho hàm số $y = f(x)$ xác định trên $\mathbb{R}$ và có bảng biến thiên như hình vẽ. Xét tính đúng sai của các khẳng định sau:
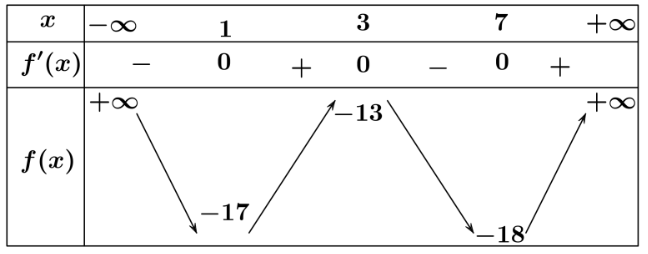
Các khẳng định:
- [T] Hàm số đồng biến trên khoảng $(7;+\infty)$.
- [T] $f(1) < f(3)$.
- [F] Hàm số nghịch biến trên khoảng $(1;7)$.
- [T] Phương trình $f’(3x-1)=0$ nhận $x = \frac{2}{3}$ làm nghiệm.
Câu 2
Cho hàm số $y = \frac{2x+1}{-x+1}$. Xét tính đúng sai của các khẳng định sau:
- [T] Hàm số đồng biến trên khoảng $(-\infty; 1)$
- [F] Hàm số nghịch biến trên khoảng $(2; +\infty)$
- [T] Hàm số đồng biến trên khoảng $(2025; 2029)$
- [F] Hàm số đồng biến trên $\mathbb{R} \setminus \{1\}$
Câu 3
Cho hàm số $y = f(x)$ xác định trên $\mathbb{R}$ và có bảng xét dấu của $f’(x)$ như hình vẽ. Xét tính đúng sai của các khẳng định sau:
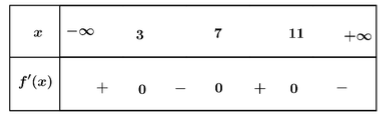
- [T] Điểm cực tiểu của hàm số đã cho là $x = 7$
- [F] $f(7)$ là giá trị cực đại của hàm số đã cho
- [F] Hàm số đồng biến trên khoảng $(7;+\infty)$
- [T] $f(11) > f(7)$
Câu 4
Cho hàm số $y = f(x)$ xác định và liên tục trên $\mathbb{R}$ có bảng biến thiên như hình vẽ dưới đây. Xét tính đúng sai của các khẳng định sau:
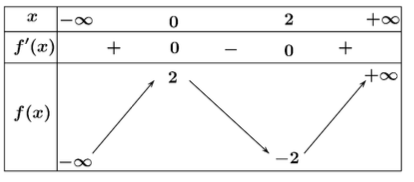
- [T] Hàm số $y = f(x)$ đồng biến trên khoảng $(-\infty;0)$ và $(2;+\infty)$
- [F] Hàm số $g(x) = 2x-3f(x)$ nghịch biến trên khoảng $(0;2)$
- [F] $f(\sin^2x) < f(\frac{3}{2})$
- [F] Hàm số $y = f(2-3x)$ nghịch biến trên khoảng $(0;2)$
Phần III: Câu trắc nghiệm trả lời ngắn
Câu 1
Cho hàm số $y = f(x) = \frac{2x^2 + 26x + 18}{x + 13}$ có cực tiểu tại $x = x_1$ và cực đại tại $x = x_2$. Tính $P = -2x_1 + x_2$.
Đáp án: 4.
Câu 2
Có bao nhiêu giá trị nguyên của $m$ để hàm số $y = \frac{mx - 3}{2x - m}$ đồng biến trên mỗi khoảng xác định của nó?
Đáp án: 5.
Câu 3
Cho hàm số $y = f(x)$ có đạo hàm $y = f’(x)$ liên tục trên $\mathbb{R}$ và có đồ thị như hình vẽ dưới đây. Hàm số $y = f(x)$ có bao nhiêu khoảng đồng biến?
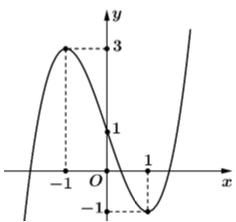
Đáp án: 2.
Câu 4
Một công ty du lịch tổ chức một chuyến đi. Giá ban đầu là 5 triệu đồng/khách cho 30 khách. Từ khách thứ 31 trở đi, cứ mỗi khách thêm thì giá giảm $a$ nghìn đồng (với $a$ là số nguyên dương). Số khách thêm tối đa là 15. Biết rằng nếu công ty nhận từ 1 đến 8 khách thêm thì tổng doanh thu tăng theo số khách thêm. Tìm giá trị nguyên lớn nhất có thể của $a$.
Đáp án: 108.
Câu 5
Tìm $m$ để hàm số $y = \frac{1}{3}x^3 - (m+1)x^2 + (m^2 + 2m)x - 3$ nghịch biến trên khoảng $(-1;1)$.
Đáp án: -1.
Câu 6
Kính viễn vọng không gian Hubble được đưa vào vũ trụ ngày 24/4/1990 bằng tàu con thoi Discovery. Vận tốc của tàu con thoi trong sứ mệnh này, từ lúc cất cánh tại thời điểm $t = 0$ (s) cho đến khi tên lửa đẩy được phóng đi tại thời điểm $t = 126$ (s) cho bởi hàm số sau đây:
$v(t) = 0,001302t^3 - 0,09029t^2 + 23$ (v đo bằng ft/s, 1 foot = 0,3048 m)
Gọi $(a;b)$ là khoảng thời gian gia tốc của tàu con thoi sẽ tăng tính từ thời điểm cất cánh cho đến khi tên lửa đẩy được phóng đi. Tính $T = a + b$?

Đáp án: 149.
Giải đáp chi tiết một số câu
Câu 4 (Eval)
a) [T] vì $f’(x)\gt 0, \forall x\in (-\infty;0)\cup(2;+\infty)$
b) [F] vì $g’(x)=2-3f(x).$ $x\in (0;2)$ nên $f’(x)\lt 0$ kéo theo $g^{\prime} (x)>0\forall x\in (0;2)$ nên $g(x)$ đồng biến.
c) [F] vì $t=\sin^2(x)\in [0;1]$, hàm số $f(t)$ nghịch biến trên $[0;2]$ do đó $f(0)\gt f(1)\gt f(\frac{3}{2})$ nên $f(\sin^{2}(x))\lt f(\frac{3}{2})$.
d) $y’=-3f(2-3x)$, $x\in (0;2)$ nên $2-3x\in (-4;2)$. Đặt $t=2-3x$ $f(t), t\in (-4;2)$. $f’(t)>0, -4<t<0$ có $y’=-3f’(t)<0, -4<t<0$. $f’(t)<0, 0<t<2$ nên $y’=-3f’(t)>0, t\in (0;2)$ $y’$ Có 2 dấu +; - nên vừa đồng biến, vừa nghịch biến trên khoảng $(0;2)$. Đáp án là sai.
Câu 5 (Fill)
$y’=x^2-2(m+1)x+(m^2+2m)$ $y’<0, \forall x\in(-1;1)$ tương đương với $\begin{cases}\triangle >0 \ x_{1}\leq -1 \leq 1\leq x_2 \end{cases}$ $y’(-1)\le 0$ và $y’(1)\le 0$. Ta có: $1+2(m+1)+(m^2+2m)\le 0$ và $1-2(m+1)+m^2+2m\le 0$. Thu gọn:
- $1+2(m+1)+(m^2+2m)\le 0$ tương đương $m^2+4m+3\le 0$ tương đương $(m+1)(m+3)\le 0$ Vậy $m\in [-3;-1]$. (1)
- $1-2(m+1)+m^2+2m\le 0$ tương đương $m^2-1\le 0$ nên $m\in [-1;1]$. (2) Kết hợp: (1) và (2) nên $m=-1$.
Câu 1 (Eval)
d)[T] $f’(3x-1)=0$ thì $3x-1\in {1;3;7}$ $x\in {\frac{2}{3}; \frac{4}{3}; \frac{8}{3}}$.
Câu 4 (Fill)
Gọi số khách là $x\in \mathbb{N}$
Ta có hàm $f(x)=\begin{cases}5x,\, x\leq 30 \ x\Big(5-(x-30).a:1000\Big), \, 31\le x\le 45 \end{cases}$ $f’(x)=\begin{cases} 5, x\le 30 \ \Big(5-(x-30).a:1000)+x\Big(0-a:1000)\Big), \, 31\le x\le 45 \end{cases}$
Hàm số $f(x)$ đồng biến $x\in [31;38]$ (1)
nghĩa là $f’(x)=\Big(5-(x-30).a:1000)+x\Big(0-a:1000)\Big)>0$ với $x\in [31;38]$.
$f’(x)=x(\frac{-2a}{1000})+5+\frac{30a}{1000}>0$
Khi $x\leq \left( 5+\frac{30a}{1000} \right):\frac{(2a)}{1000}$ (2)
Từ (1) và (2) thì $38 \le \left( 5+\frac{30a}{1000} \right):\frac{(2a)}{1000}$.