Chương 1. Ứng dụng đạo hàm

Bài 3. Tiệm cận của đồ thị hàm số

PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn

Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1

Tiệm cận ngang của đồ thị hàm số $y = \frac{3x+1}{x-1}$ có phương trình:

• $y = \frac{1}{3}$
• $y = 3$
• $y = -1$
• $y = 1$

Câu 2

Tiệm cận đứng của đồ thị hàm số $y = \frac{2x-2}{x+1}$ là đường thẳng nào sau đây?

• $x = -2$
• $x = 1$
• $x = -1$
• $x = 2$

Câu 3

Cho hàm số $y = f(x)$ có $\lim\limits_{x \to +\infty} f(x) = 1$ và $\lim\limits_{x \to -\infty} f(x) = -1$. Khẳng định nào sau đây là khẳng định đúng?

• Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng $x = 1$ và $x = -1$.
• Đồ thị hàm số đã cho không có tiệm cận ngang.
• Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
• Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng $y = 1$ và $y = -1$.

Câu 4

Cho hàm số $y = f(x)$ có bảng biến thiên như sau. Tổng số đường tiệm cận ngang và đường tiệm cận đứng của đồ thị hàm số đã cho là:

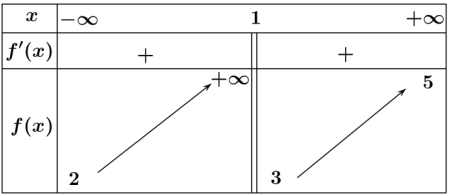
• 3
• 2
• 4
• 1

Câu 5

Hàm số nào sau đây có một tiệm cận:

• $y = \dfrac{x+3}{2x-1}$
• $y = \dfrac{x^2 + 3x - 2}{x+3}$
• $y = \dfrac{4}{x-1}$
• $y = \dfrac{2x}{x^2 + 1}$

Câu 6

Cho hàm số $y = f(x)$ có bảng biến thiên như sau. Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:

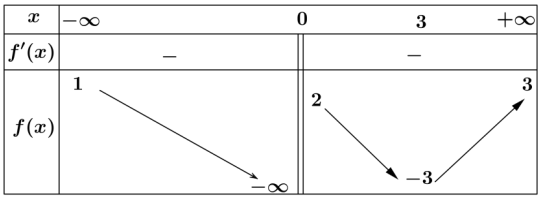
• 2
• 3
• 4
• 1

Câu 7

Đường thẳng $2y + 1 = 0$ là tiệm cận ngang của hàm số nào sau đây?

• $y = \frac{x+1}{2x+1}$
• $y = \dfrac{x^2 + x + 1}{1-2x}$
• $y = \dfrac{2x+1}{1-x}$
• [x ] $y = \dfrac{3-x^2}{2x^2 - 3x + 1}$

Câu 8

Cho hàm số $y = 2x - 1 + \dfrac{3}{x+3} \ (C)$. Khoảng cách từ $M(2; -1)$ đến tiệm cận xiên của đồ thị $(C)$ là:

• $\dfrac{2}{\sqrt{5}}$
• $\dfrac{4}{\sqrt{5}}$
• 2
• 4

Câu 9

Với giá trị nào của $m$ thì tiệm cận xiên của đồ thị hàm số $y = x + m + \dfrac{3}{m-x}$ đi qua điểm $M(1;2)$

• $m = 1$
• $m = 0$
• $m = 2$
• Một đáp án khác.

Câu 10

Đồ thị hàm số $y = \dfrac{2x^2 - 3x + m}{x-m}$ là $(C_m)$. Giá trị của $m$ để đồ thị hàm số $(C_m)$ không có tiệm cận đứng là:

• $m = 0$
• $m = 1$
• $m = 0$ hoặc $m = 1$
• $m = 0$ hoặc $m = -1$.

Câu 11

Cho hàm số $y = \frac{mx^2 + 6x - 2}{x+2}$ có đồ thị $(C_m)$. Với giá trị nào của $m$ thì đồ thị hàm số $(C_m)$ có tiệm cận đứng và không có tiệm cận xiên.

• $m = \frac{7}{2}$
• $m = \frac{3}{2}$
• $m = 2$
• $m = 0$

Câu 12

Tại một công ty sản xuất đồ chơi $A$, công ty phải chi $50000$ USD để thiết lập dây chuyền sản xuất ban đầu. Sau đó, cứ sản xuất được một sản phẩm đồ chơi $A$, công ty phải chi trả $5$ USD cho nguyên liệu thô và nhân công. Gọi $x \ (x \geq 1)$ là số đồ chơi $A$ mà công ty đã sản xuất và $T(x)$ (đơn vị USD) là tổng số tiền bao gồm cả chi phí ban đầu mà công ty phải chi trả khi sản xuất $x$ đồ chơi $A$. Người ta xác định chi phí trung bình cho mỗi sản phẩm đồ chơi $A$ là $M(x) = \frac{T(x)}{x}$.

Khi $x$ đủ lớn $(x \to +\infty)$ thì chi phí trung bình (USD) cho mỗi sản phẩm đồ chơi $A$ gần nhất với kết quả nào sau đây?

• $50000$
• $50005$
• $10$
• $5$

PHẦN II. Câu trắc nghiệm đúng sai

Câu 1

Cho hàm số $y = f(x)$ có bảng biến thiên như hàm số dưới đây. Xét tính đúng sai của các khẳng định sau:

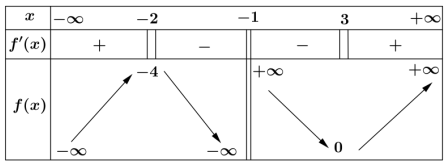
• [F] Hàm số đã cho nghịch biến trên khoảng $(-2; 0)$

• [F] Đồ thị hàm số đã cho có tiệm cận ngang

• [F] Đồ thị hàm số đã cho có hai đường tiệm cận đứng

• [F] Hàm số có giá trị lớn nhất trên $\mathbb{R}$

Câu 2

Cho hàm số có đồ thị như hình vẽ dưới đây. Xét tính đúng sai của các khẳng định sau:

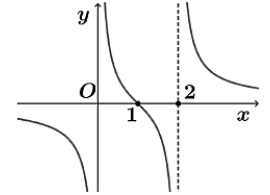
• [T] Hàm số đã cho liên tục trên khoảng $(0; 2)$

• [T] Hàm số đã cho nghịch biến trên khoảng $(1; 2)$

• [T] Đồ thị hàm số đã cho không có đường tiệm cận ngang

• [T] Khoảng cách giữa hai đường tiệm cận đứng của đồ thị hàm số bằng $2$.

Câu 3

Cho hàm số $y = \frac{x^2 - 2x + 2}{x + 2}$ có đồ thị là $(C)$. Xét tính đúng sai của các khẳng định sau:

• [T] Đồ thị hàm số $(C)$ có hai đường tiệm cận.

• [T] Giao điểm của hai tiệm cận là $I(-2; -6)$.

• [F] Khoảng cách từ $O$ đến tiệm cận xiên bằng $4\sqrt{2}$.

• [T] Đường tiệm cận xiên của đồ thị hàm số $(C)$ đi qua điểm $M(0; -4)$.

Câu 4

Cho hàm số $y = \frac{x^2 + mx - 1}{x - 1} \ (C_m) \ (m \text{ là tham số})$. Xét tính đúng sai của các khẳng định sau:

• [T] Để đồ thị $(C_m)$ của hàm số có tiệm cận xiên thì $m \neq 0$.

• [T] Để tiệm cận xiên của $(C_m)$ đi qua $M(2; -5)$ thì $m = -8$.

• [F] Để tiệm cận xiên của $(C_m)$ tạo với hai trục tọa độ một tam giác có diện tích bằng $8$ (đvdt) thì tổng tất cả các giá trị $m$ tìm được bằng $2$.

• [F] Với $m = 3$ thì giao điểm của hai đường tiệm cận của $(C_m)$ nằm trên Parabol $y = x^2 + 3$.

PHẦN III. Câu trắc nghiệm trả lời ngắn

Câu 1

Cho hàm số $y = \frac{2x + m}{mx - 1}$. Tổng các giá trị $m$ để đồ thị hàm số có tiệm cận đứng, tiệm cận ngang và các tiệm cận cùng với hai trục tọa độ tạo thành một hình chữ nhật có diện tích là $2$.

Đáp án: 0.

Câu 2

Chi phí để loại bỏ $x\%$ chất gây ô nhiễm là $C$ (nghìn đô) với $C(x) = \frac{12x}{100-x}$. Tính chi phí để loại bỏ $50\%$ chất gây ô nhiễm?

Đáp án: 12000.

Câu 3

Anh An là một nhà quy hoạch đô thị, mô hình hóa dân số $P(t)$ (nghìn người) của vùng anh ấy sống sau $t$ năm kể từ thời điểm hiện tại là $P(t) = \dfrac{40t}{t^2 + 10} - \dfrac{50}{t + 1} + 70$. Dân số mà anh An dự kiến trong dài hạn là bao nhiêu nghìn người (khi $t \to +\infty$).

Đáp án: 70.

Câu 4

Nồng độ thuốc trong máu của một bệnh nhân $t$ giờ sau khi tiêm là $C(t) \left[ \frac{mg}{ml} \right]$ với $C(t)$ được cho bởi công thức $C(t) = \frac{0.4}{t^2 + 1} + 0.013$. Tìm nồng độ thuốc tồn dư, tức là nồng độ thuốc vẫn còn trong cơ thể bệnh nhân trong dài hạn (khi $t \to +\infty$).

Đáp án: 0.013.

Câu 5

Hai loài cùng tồn tại trong cùng một hệ sinh thái. Sau $t$ năm, số lượng cá thể loài $I$ là $P(t)$ nghìn con, số lượng cá thể loài $II$ là $Q(t)$ nghìn con, trong đó $P$ và $Q$ được mô hình hóa bởi các hàm $Q(t) = \dfrac{64}{4 - t}$ với mọi $t \geq 0$ sao cho số lượng cá thể tương ứng là đại lượng không âm. Tìm số lượng cá thể ban đầu của mỗi loài $II$.

Đáp án: 16.

Câu 6

Cho hàm số $y = \frac{mx^2 + (m^2 + m + 2)x + m^2 + 3}{x + 1}$. Tìm $m \in \mathbb{R}$ để khoảng cách từ gốc $O$ đến tiệm cận xiên hoặc ngang là nhỏ nhất.

Đáp án: 2.