Toán 9

Chương I. Phương trình và hệ hai phương trình bậc nhất hai ẩn

Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn.

1. Phương trình bậc nhất hai ẩn

Định nghĩa: Phương trình bậc nhất hai ẩn có dạng: $ax+by=c,$ trong đó $a^2+b^2>0$

(điều kiện $a\neq 0$ hoặc $b\neq 0$ tương đương với $a^2+b^2>0$)

Trường hợp 1. $a=0$

Phương trình $ax+by=c$ trở thành $by=c$ hay $y=\frac{c}{b}$.
Tập nghiệm của phương trình $\begin{cases} x\in \mathbb{R} \\ y= \frac{c}{b} \end{cases}$

Trường hợp 2. $b=0$

Phương trình $ax+by=c$ trở thành $ax=c$ hay $x=\frac{c}{a}$.
Tập nghiệm của phương trình $\begin{cases} x= \frac{c}{a} \\ y\in \mathbb{R} \end{cases}$

Trường hợp 3. $a\neq 0$ và $b\neq 0$

Phương trình $ax+by=c$ trở thành $y=-\frac{a}{b}x+\frac{c}{b}$.
Tập nghiệm của phương trình $\begin{cases} x\in \mathbb{R} \\ y=-\frac{a}{b}x+\frac{c}{b} \end{cases}$

Chú ý: Phương trình bậc nhất hai ẩn luôn có vô số nghiệm.

Ví dụ 2: Giả sử $(x,y)$ là nghiệm của phương trình bậc nhất hai ẩn $x+2y=5.$

a) Hoàn thành bảng sau:

$x$	$-2$	$-1$	$0$	$x+2.1=5$	$x+2.2=5$
$y$	$-2+2y=5$	$-1+2y=5$	$0+2y=5$	$1$	$2$
	$2y=7$	$2y=6$	$2y=5$	$x+2=5$	$x+4=5$
	$y=\dfrac{7}{2}$	$y=3$	$y=\dfrac{5}{2}$	$x=3$	$x=1$

Rút ra được: Có $x$ thì sẽ tìm được $y$ và ngược lại.

b) Tính $y$ theo $x$. Từ đó cho biết phương trình đã cho có bao nhiêu nghiệm?

$y=\dfrac{5-x}{2},$ $x\in \mathbb{R}$ nên phương trình đã cho có vô số nghiệm.

2. Biểu diễn nghiệm của phương trình bậc nhất 2 ẩn.

Trường hợp 1. $a=0$

Phương trình $ax+by=c$ trở thành $by=c$ hay $y=\frac{c}{b}$.

Ví dụ: Với $b=1, c= 2$ thì $y=2$. Nghiệm của phương trình $0x+y=2$ có dạng $(x_0,2)$, các điểm có toạ độ $(x_0,2)$ biểu diễn trên mặt phẳng $(Oxy)$ là đường thẳng $y=2$ song song với trục hoành ($Ox$) và cắt trục tung ($Oy$) tại điểm $(0,2)$.

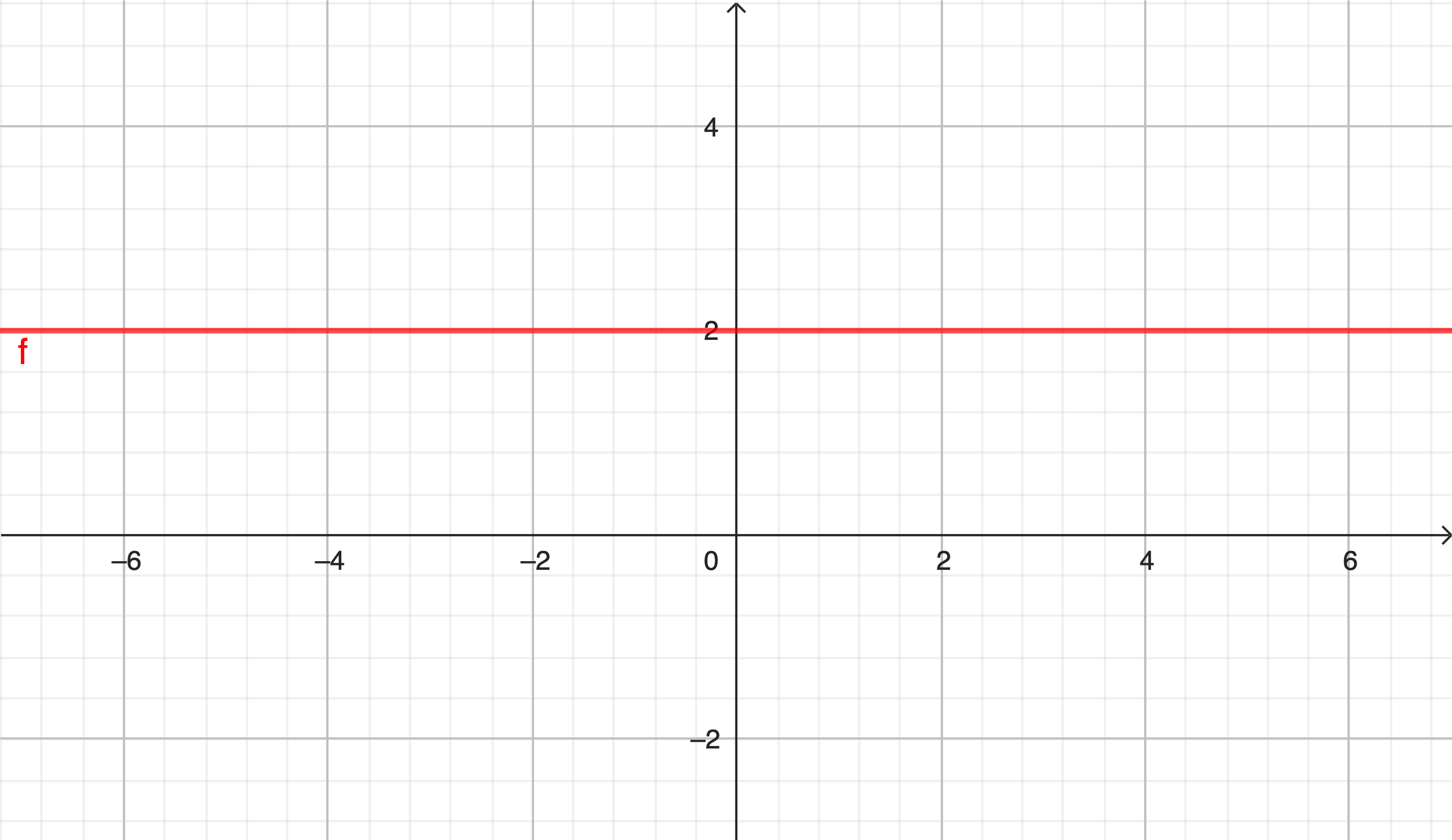
Trường hợp 2. $b=0$

Phương trình $ax+by=c$ trở thành $ax=c$ hay $x=\frac{c}{a}$.

Ví dụ: Với $a=1, c= 2$ thì $x=2$. Nghiệm của phương trình $x+0y=2$ có dạng $(2,y_0)$, các điểm có toạ độ $(2,y_0)$ biểu diễn trên mặt phẳng $(Oxy)$ là đường thẳng $x=2$ song song với trục tung ($Oy$) và cắt trục hoành ($Ox$) tại điểm $(2,0)$.

Trường hợp 3. $a\neq 0$ và $b\neq 0$

Phương trình $ax+by=c$ trở thành $y=-\frac{a}{b}x+\frac{c}{b}$.

Ví dụ: Với $a=1, b=1, c= 2$ thì $y=-\frac{1}{1}x+\frac{2}{1}$ hay $y=-x+2$. Nghiệm của phương trình $x+y=2$ có dạng $(x_0,2-x_0)$, các điểm có toạ độ $(x_0,2-x_0)$ biểu diễn trên mặt phẳng $(Oxy)$ là đường thẳng $y=-x+2$ cắt trục hoành ($Ox$) tại điểm $(2,0)$ và cắt trục tung ($Oy$) tại điểm $(0,2)$.

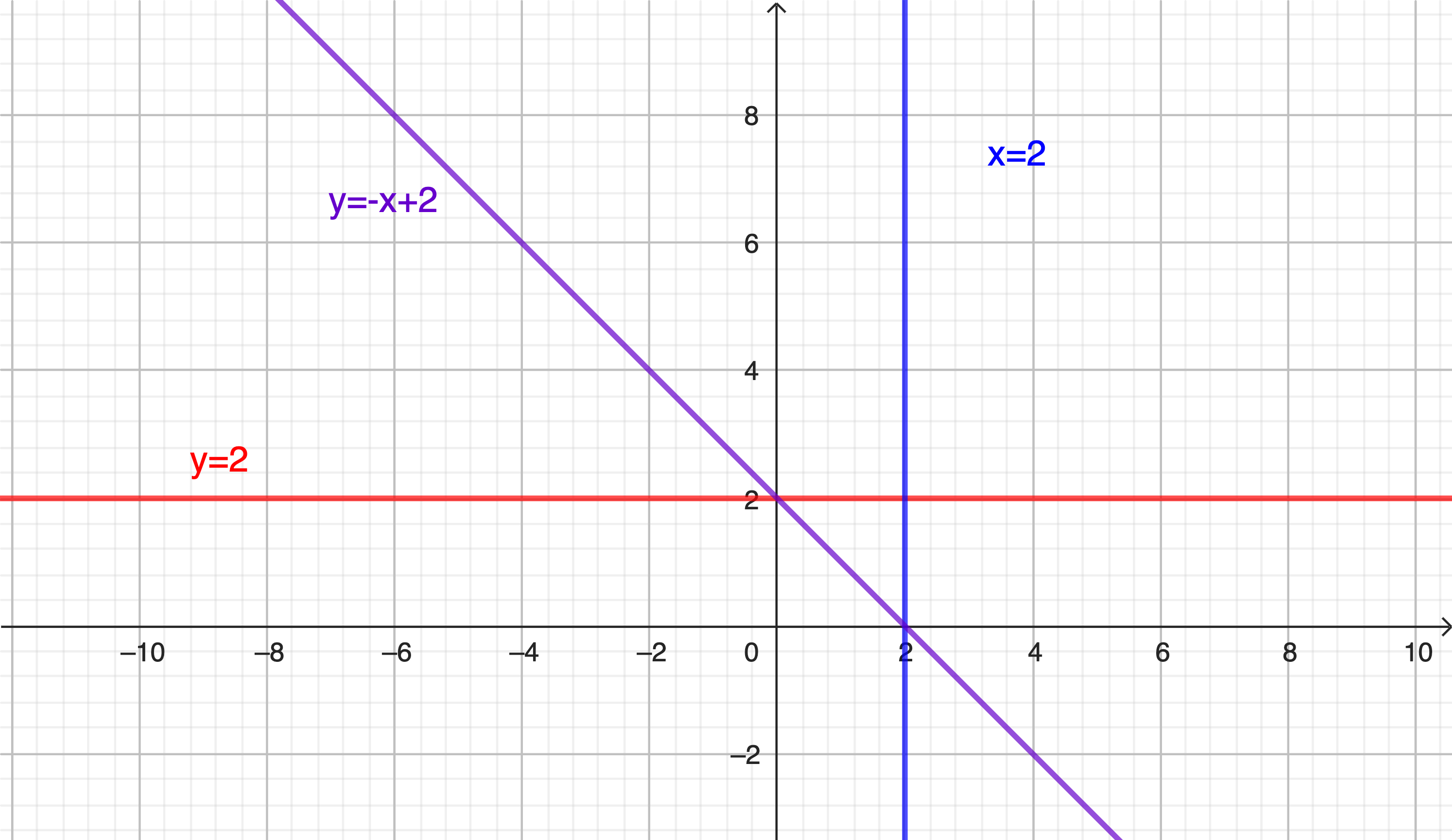
Chú ý:

Tập nghiệm có thể mô tả bằng đường thẳng
Khi $a\neq 0$ và $b\neq 0$, ta rút $y$ theo $x$ biểu thức $y= -\frac{a}{b}x+\frac{c}{b}$ giống như dạng hàm số bậc nhất.
Cần có kĩ năng vẽ đồ thị hàm số bậc nhất: Lấy 2 điểm phụ. </span>

2. Hệ hai phương trình bậc nhất hai ẩn

Định nghĩa: Một cặp gồm hai phương trình bậc nhất hai ẩn $ax+by=c$ và $a'x+b'y=c'$ được gọi là một hệ hai phương trình bậc nhất hai ẩn. Kí hiệu

\[\begin{cases} ax+by=c \\ a'x+b'y=c' \end{cases}\]

Chú ý: $\{$ thường được gọi là “và” (tô đỏ trong định nghĩa)

Mỗi cặp số $(x_0,y_0)$ được gọi là một nghiệm của hệ nếu nó đồng thời là nghiệm của cả hai phương trình.

Ví dụ: Trong các hệ phương trình sau, hệ nào không phải là hệ hai phương trình bậc nhất hai ẩn, vì sao?

\[\begin{cases}2x=6 \\ 5x+4y=1 \end{cases}\quad \begin{cases} x+2y=-3 \\ 0x+0y=1 \end{cases} \quad \begin{cases} 3x-y=1 \\ x+y=3 \end{cases}\]

(Nhận dạng hệ phương trình bậc nhất 1 ẩn: 2 phương trình phải là 2 phương trình bậc nhất 1 ẩn ($a^2+b^2>0, a'^2+b'^2>0$))

Ví dụ: Giải thích tại sao cặp số $(1;2)$ là một nghiệm của hệ phương trình $\begin{cases} 2x-y=0 \\ x+y=3 \end{cases}$

Thay $x=1, y=2$ vào hệ phương trình (cách nhanh nhất)

Mỗi phương trình có tập nghiệm được biễu diễn bằng đường thẳng.
Nghiệm của hệ là giao điểm của 2 đường thẳng.
Sự liên hệ giữa nghiệm của hệ phương trình và giao điểm của 2 đường thẳng:

Vị tương đối của 2 đường thẳng	Nghiệm của hệ	Điều kiện
Song song	Vô nghiệm	$\frac{a}{a'}=\frac{b}{b'}\neq \frac{c}{c'}$
Cắt nhau	1 nghiệm	$\frac{a}{a'}\neq \frac{b}{b'}$
Trùng nhau	Vô số nghiệm	$\frac{a}{a'}=\frac{b}{b'}=\frac{c}{c'}$

3. Phương pháp giải hệ:

Có 2 phương pháp: Phương pháp cộng đại số và phương pháp thế. (Sách giáo khoa rất dễ hiểu)

Về Trang chủ